Introduction
Viper is a verification infrastructure that simplifies the development of program verifiers and facilitates rapid prototyping of verification techniques and tools. In contrast to similar infrastructures such as Boogie and Why3, Viper has strong support for permission logics such as separation logic and implicit dynamic frames. It supports permissions natively and uses them to express ownership of heap locations, which is useful to reason about heap-manipulating programs and thread interactions in concurrent software.
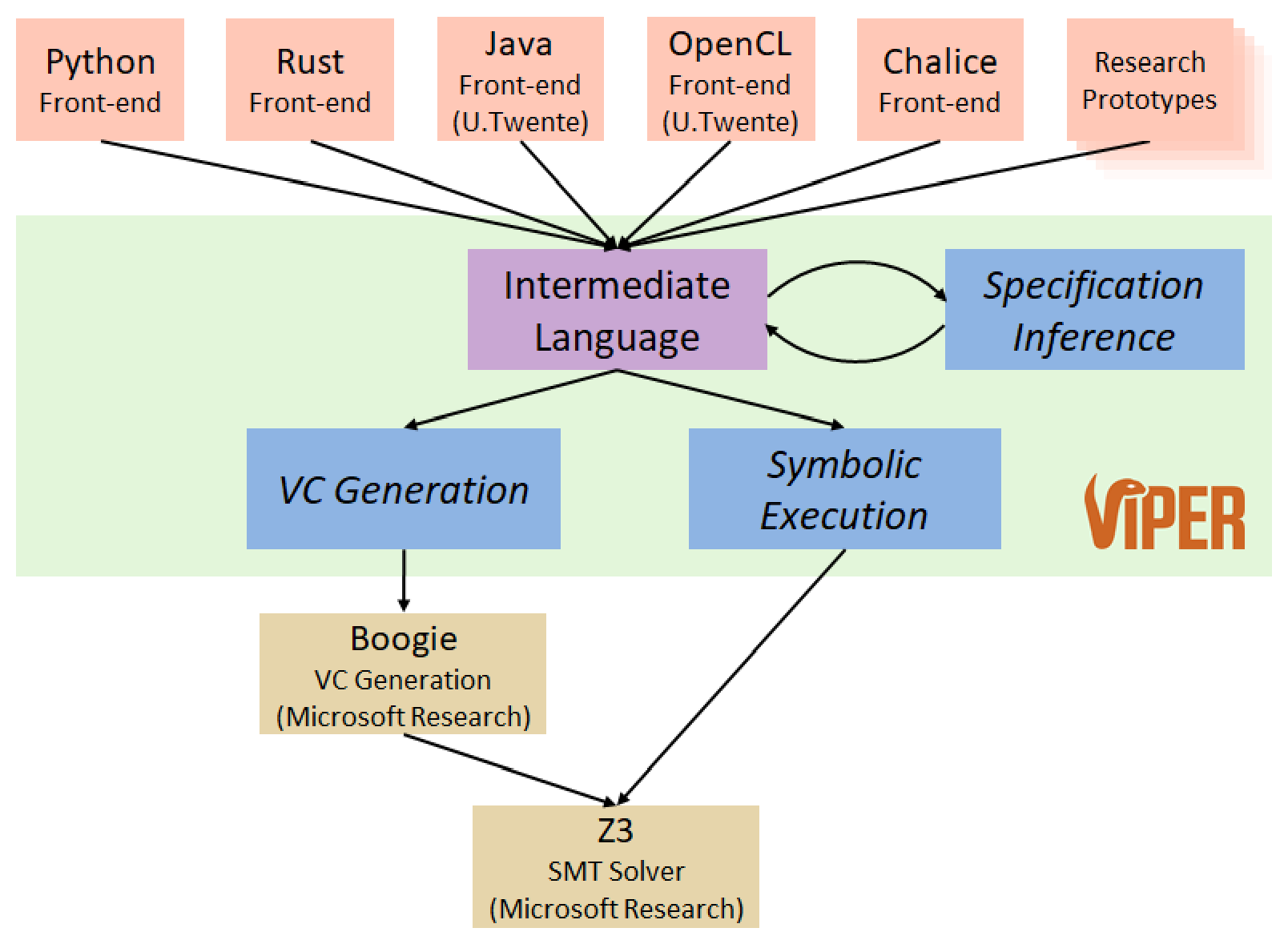
The Viper infrastructure, shown above, provides an intermediate language as well as two verification back-ends, one based on symbolic execution and one based on verification condition generation. Both back-ends ultimately use the SMT solver Z3 to discharge proof obligations. Front-end tools translate different source languages and verification approaches into the Viper language and thereby benefit from its tool support and automation.
The Viper intermediate language is a simple sequential, object-based, imperative programming language. Even though it has been designed as an intermediate language, the Viper language supports both high-level features that are convenient to express verification problems manually as well as powerful low-level features that are useful to encode source languages and verification techniques automatically.
The following simple example shows a method that computes the sum of the first n positive natural numbers. The method declaration includes a precondition (the assertion following requires) to restrict the argument to non-negative values. This expresses the fact that method sum can only be assumed to behave correctly (in particular, do not crash) for non-negative values. The method declaration also includes a postcondition (the assertion following ensures) to guarantee properties of the result variable res. The postcondition is the only information that a caller of the method sum can use to correlate the call result and argument. In particular, in absence of post-condition a caller of method sum cannot make use of the fact that the result is non-negative. This would be required, for example, in order to be able to call sum on its own result. Method preconditions and postconditions together make up a method’s specification.
Viper verifies partial correctness of program statements; that is, verification guarantees that if a program state is reached, then the properties specified at that program state are guaranteed to hold. For example, the postcondition of sum is guaranteed to hold whenever a call to sum terminates. Verification of loops also requires specification: the loop in sum‘s body needs a loop invariant (if omitted, the default loop invariant is true, which is typically not strong enough to prove interesting properties of the program). The loop invariant in sum could also be written in one line with the boolean operator && placed between the two assertions.
method sum(n: Int) returns (res: Int)
requires 0 <= n
ensures res == n * (n + 1) / 2
{
res := 0
var i: Int := 0;
while(i <= n)
invariant i <= (n + 1)
invariant res == (i - 1) * i / 2
{
res := res + i
i := i + 1
}
}
- This tutorial features runnable examples, which use the Viper verifiers. You can run the example by hitting the “play” button - it should verify without errors.
- You can also edit the examples freely, and try out your own versions. Try commenting the
requiresline (the method precondition) - this should result in a verification error. Viper supports both//and/* ... */styles for comments. - Try implementing a recursive version of the
summethod. Note that Viper does not allow method calls within compound expressions; a call tosummust have the formx := sum(e)for some variablexand expressione, and not, e.gx := sum(e) + 42. Does the same specification work also for your recursive implementation? - Try implementing client code which calls the
summethod in order to computes the sum of the first 5 natural numbers. Provide a suitable postcondition.
This tutorial gives an overview of the features of the Viper language and explains their syntax and semantics. We provide examples and exercises throughout, to illustrate the basic usage of these features. We encourage readers to experiment with the examples and often suggest variations of the presented examples to try out. The tutorial does not aim to explain the workings of the Viper verifiers in general, nor the advanced usage of Viper’s language features for building custom verification tools: for these topics, we refer interested readers to our Viper-related research papers.
If you have comments, questions or feedback about Viper, including this tutorial, we would be happy to receive them! Please send your emails to viper@inf.ethz.ch
Structure of Viper Programs
For a type safe Viper program to be correct, all methods and functions in it must be successfully verified against their specifications. The implementation of a Viper method consists of certain imperative building blocks (such as branch conditions, loops, etc.) whereas the specification consists of assertions (contracts, loop invariants, etc.). Statements (or operations) may change the program state, whereas assertions cannot. In contrast, assertions can talk about properties of a particular state — so they can be used to specify the behavior of operations. What the implementation and the specification have in common is that they both make use of expressions. For all of these building blocks, Viper supports different means of abstraction.
Methods can be viewed as a means of abstraction over a sequence of operations (i.e. the execution of a potentially-unbounded number of statements). The caller of a method observes its behavior exclusively through the method’s signature and its specification (its preconditions and postconditions). Viper method calls are treated modularly: for the caller of a method, the method’s implementation can be thought of as invisible. Calling a method may result in modifications to the program state, therefore method calls cannot be used in specifications. On the one hand, the caller of a method must first satisfy the assertions in its precondition in order to obtain the assertions from its postcondition. On the other hand, in order to verify a method itself, Viper must prove that the method’s implementation adheres to the method’s specification.
Functions can be viewed as a means of abstraction over (potentially state-dependent) expressions. Generally, the caller of a function observes three things. First, the precondition of the function is checked in the state in which the function is called. The precondition may include assertions denoting resources, such as permissions to field locations that the the function may read from. Second, the function application’s result value is equated with the expression in the function’s body (if provided); note that this usage of the function’s implementation is a difference from the handling of methods. Third, the function’s postconditions are assumed. The postcondition of a function may not contain resource assertions (e.g. denoting field permissions): all resources from the precondition are automatically returned after the function application. Refer to the section on functions for more details.
Predicates can be viewed as a means of abstraction over assertions (including resources such as field permissions). The body of a predicate is an assertion. Unlike functions, predicates are not automatically inlined: to replace a predicate with its body, Viper provides an explicit unfold statement. An unfold is an operation that changes the program state, replacing the predicate resource with the assertions specified by its body. The dual operation is called a fold: folding a predicate replaces the resources specified by its body with an instance of the predicate itself. Refer to the section on predicates for more details.
Below you can find a brief description and examples of the language constructs that can be used to write a Viper program. Note that the order in which top-level declarations are written is not important, as names are resolved against all declarations of the program (including later declarations).
Language overview
Top-level declarations
Fields
field val: Int
field next: Ref
- Declared by keyword
field - Every object has all fields (there are no classes in Viper)
- See the permission section for examples
Methods
method QSort(xs: Seq[Ref]) returns (ys: Seq[Ref])
requires ... // precondition
ensures ... // postcondition
{
// body (optional)
}
- Declared by keyword
method - Have input and output parameters (e.g.,
xsandys) - Method calls can modify the program state; see the section on statements for details
- Hence calls cannot be used in specifications
- Modular verification of methods and method calls
- The body may include some number of statements (including recursive calls)
- The body is invisible at call site (changing the body does not affect client code)
- The precondition is checked before the method call (more precisely, it is exhaled)
- The postcondition is assumed after the method call (more precisely, it is inhaled)
- See the permission section for more details and examples
Functions
function gte(x: Ref, a: Int): Int
requires ... // precondition
ensures ... // postcondition
{
... // body (optional)
}
- Declared by keyword
function - Have input parameters (e.g.,
xanda) and one output return value - The keyword
resultmay be used in a function’s postcondition to refer to the return value - Function applications may read but not modify the program state
- Function applications can be used in specifications
- Permissions (and resource assertions in general) may be mentioned in a function’s precondition, but not in its postcondition
- If a function has a body, the body is a single expression (possibly including recursive calls to functions)
- Unlike methods, function applications are not handled modularly (for functions with bodies): changing the body of a function affects client code
- See the section on functions for details
Predicates
predicate list(this: Ref) {
... // body (optional)
}
- Declared by keyword
predicate - Have input parameters (e.g.,
head) - Typically used to abstract over assertions and to specify the shape of recursive data structures
- Predicate instances (e.g.
list(x)) are resource assertions in Viper - See the section on predicates for details
Domains
domain Pair[A, B] {
function getFirst(p: Pair[A, B]): A
// other functions
axiom ax_1 {
... // axiom body
}
// other axioms
}
- Declared by keyword
domain - Have a name, which is introduced as an additional type in the Viper program
- Domains may have type parameters (e.g.
AandBabove) - A domain’s body (delimited by braces) consists of a number function declarations, followed by a number of axioms
- Domain functions (functions declared inside a
domain) may have neither a body nor a specification; these are uninterpreted total mathematical functions - Domain axioms consist of name (following the
axiomkeyword), and a definition enclosed within braces (which is a boolean expression which may not read the program state in any way)
- Domain functions (functions declared inside a
- Useful for specifying custom mathematical theories
- See the section on domains for details
Macros
define plus(a, b) (a+b)
define link(x, y) {
assert x.next == null
x.next := y
}
- Declared by keyword
define - C-style, syntactically expanded macros
- Macros are not type-checked until after expansion
- However, macro bodies must be well-formed assertions / statements
- May have any number of (untyped) parameter names (e.g.
aandbabove) - The are two kinds of macros
- Macros defining assertions (or expressions) include the macro definition whitespace-separated afterwards (e.g.
plusabove) - Macros defining statements include their definitions within braces (e.g.
linkabove)
- Macros defining assertions (or expressions) include the macro definition whitespace-separated afterwards (e.g.
- See the array domain encoding for an example
Built-in types
Reffor references (to objects, except for the built-inRefconstantnull)Boolfor Boolean valuesIntfor mathematical (unbounded) integersRationalfor mathematical (unbounded) rationals (this type is expected to be deprecated in the summer 2023 release)Permfor permission amounts (see the section on permissions for details)Seq[T]for immutable sequences with element typeTSet[T]for immutable sets with element typeTMultiset[T]for immutable multisets with element typeTMap[T, V]for immutable maps with key typeTand value typeV- Additional types can be defined via domains
Imports
Local Import:
import "path/to/local.vpr"
Standard Import:
import <path/to/provided.vpr>
Imports provide a simple mechanism for splitting a Viper program across several source files using the local import. Further, it also makes it possible to make use of programs provided by Viper using the standard import.
- A relative or absolute path to a Viper file may be used (according to the Java/Unix style)
importadds the imported program as a preamble to the current one- Transitive imports are supported and resolved via depth-first traversal of the import graph
- The depth-first traversal mechanism enforces that each Viper file is imported at most once, including in the cases of multiple (indirect) imports of the same file or of recursive imports.
Permissions
Introduction
Reasoning about the heap of a Viper program is governed by field permissions, which specify the heap locations that a statement, an expression or an assertion may access (read and/or modify).
Heap locations can be accessed only if the corresponding permission is held by the currently verified method. The simplest form of field permission is the exclusive permission to a heap location x.f; it expresses that the current method may read and write to the location, whereas other methods or threads are not allowed to access it in any way.
Every Viper operation, i.e., every statement, expression, or assertion, has an implicit or explicit specification expressing which field permissions the operation requires, i.e., which locations it accesses. The part of the heap denoted this way is called the footprint of an operation.
Permissions enable preserving information about heap values in Viper: as long as the footprint of an expression is disjoint from the footprint of a method call, it can be concluded that the call does not change the expression’s value, even if the concrete method implementation is unknown. Preserving properties this way is called framing: e.g. we might say that the value of an expression is framed across a method call, or in general, across a statement.
For example: the footprints of the expression x.f == 0 and the field assignment statement x.f := 1 are not disjoint, and the property x.f == 0 can therefore not be framed across the assignment. In contrast, the property could be framed across y.f := 0 if y and x were known to not be aliases. Permissions can also be used to guarantee non-aliasing, as will be discussed in more detail later.
In pre- and postconditions, and generally in assertions, permission to a field is denoted by an accessibility predicate: an assertion which is written acc(x.f). An accessibility predicate in a method’s precondition can be understood as an obligation for a caller to transfer the permission to the callee, thereby giving it up. Consequently, an accessibility predicate in a postcondition can be understood as a permission transfer in the opposite direction: from callee to caller.
A simple example is given next: a method inc that increments the field x.f by an arbitrary value i.
field f : Int
method inc(x: Ref, i: Int)
requires acc(x.f)
ensures true
{
x.f := x.f + i
}
The program above declares a single integer (Int) field f, and the aforementioned increment method. The reference type (Ref) is built in; values of this type (other than the special value null) represent objects in Viper, which are the possible receivers for field accesses. Method inc‘s specification (sometimes called its contract, in other languages) is expressed via its precondition (requires) and postcondition (ensures).
- You can run the example by hitting the “play” button - it should verify without errors.
- Comment out the
requiresline (the method precondition) and re-run the example - this will result in a verification error, since permission to accessx.fis no longer guaranteed to be held. - Implement an additional method that requires permission to
x.fin its precondition and callsinc(x, 0)twice in its body. Does the current specification ofincsuffice here? Can you guess what the problem is, and solve it?
In the remainder of this section we proceed as follows: After a brief description of Viper’s program state, we introduce the basic permission-related features employed by Viper. In particular, we discuss permission-related statements in the Viper language, as well as permission-related assertions, when such assertions are well-defined, and how they can be used to specify properties such as (non-)aliasing. Finally, we present a refined notion of permission supported by Viper: fractional permissions, which enable simultaneous access to the same heap location by multiple methods or (when modelling these in Viper) concurrent threads.
Viper’s Program State
Permissions are a part of a Viper program’s state, alongside the values of variables and heap locations. Fields are only the first of several kinds of resource that will be explained in this tutorial; access to each resource is governed by appropriate permissions. Different permissions can be held at different points in a Viper program: e.g., after allocating new memory on the heap, we would typically also add the permission to access those locations. In the next subsection, we will see the primitive operations Viper provides for manipulating the permissions currently held.
A program state in Viper consists of:
- The values of all variables in scope: these include local variables, method input parameters (which cannot be assigned to in Viper), and method return parameters (which can) of the current method execution. Verification in Viper is method-modular: each method implementation is verified in isolation and, thus, the program state does not contain an explicit call stack.
- The permissions to field locations held by the current method execution.
- The values of those field locations to which permissions are currently held. Other field locations cannot be accessed.
The initial state of each method execution contains arbitrary values (of the appropriate types) for all variables in scope, and no permissions to heap locations. Permissions can be obtained through a suitable precondition (as in the inc example above); preconditions can also constrain the values of parameters and heap locations. Field locations to which permission is newly obtained will also contain arbitrary values.
Inhaling and Exhaling
As previously mentioned, accessibility predicates in a method’s precondition, such as acc(x.f) in the precondition of inc, can be understood as specifying that permission to a field (here x.f) must be transferred from caller to callee.
The process of gaining permission (which happens in the callee), is called inhaling permissions; the opposite process of losing permission (in the caller) is called exhaling. Both operations thus update the amount of currently held permissions: from a caller’s perspective, permissions required by a precondition are removed before the call and permissions guaranteed by a postcondition are gained after the call returns. From a callee’s perspective, the opposite happens.
Similar permission transfers also happen at other points in a Viper program; most notably, when verifying loops: a loop invariant specifies the permissions transferred (1) from the enclosing context to the first loop iteration, (2) from one loop iteration to the next, and (3) from the last loop iteration back to the enclosing context. Inside a loop body, heap locations may only be accessed if the required permissions have been explicitly transferred from the surrounding context to the loop body via the loop invariant.
In addition to specifying which permissions to transfer, Viper assertions may also specify constraints on values, just like in traditional specification languages. For example, a precondition acc(x.f) && x.f > 0 requires permission to location x.f and that its value is positive. Note that the occurrence of x.f inside acc(x.f) denotes the location (in compiler parlance, x.f as an lvalue); the meaning of an accessibility predicate is independent of the value of x.f as an expression (as used, e.g., in x.f > 0).
Consider now the call in the first line of method client in the example below: set‘s precondition specifies that the permission to a.f is transferred from the caller to the callee, and that i must be greater than a.f. Thus, method client has to exhale the permission to a.f (which is inhaled by set) and the caller has to prove that a.f < i (which it currently cannot). Conversely, the postcondition causes the permission to be transferred back to the caller when set terminates, i.e., it is inhaled by method client, and the caller gains the knowledge that a.f == 5.
When verifying method set itself, the opposite happens: permission to x.f is inhaled before the method body is verified, alongside the fact that x.f < i. After the body has been verified, permission to x.f are exhaled and it is checked that x.f‘s value is indeed i.
field f: Int
method client(a: Ref)
requires acc(a.f)
{
set(a, 5)
a.f := 6
}
method set(x: Ref, i: Int)
requires acc(x.f) && x.f < i
ensures acc(x.f) && x.f == i
{
x.f := i
}
- Method
clientfails to verify: the precondition of the callset(a, 5)may not hold. Can you fix this (without modifying methodset)? - Afterwards, add the following call as the last statement to method
client:set(a, a.f). Verification will now fail again. Remedy the situation by slightly weakening methodset‘s precondition. - Finally, comment out the postcondition of method
set. Verification will fail again because methodclientdoes not have permission for the assignment toa.f. When a method call terminates, all remaining permissions that are not transferred back to its caller (via its postcondition) are leaked (lost).
Note that when encoding, e.g., a garbage-collected source language into Viper, the design choice that any excess permissions get leaked is convenient; it allows heap-based data to simply go out of scope and become unreachable. However, in the case of set in the example above, such leaking is presumably not the intention. Viper can also be used to check that certain permissions are not leaked; see the perm expression in the section on expressions for more details.
Inhale and Exhale Statements
To enable the encoding of programming language features that are not directly supported by Viper, such as forking and joining threads or acquiring and releasing locks, Viper allows one to explicitly exhale or inhale permissions via the statements exhale A and inhale A, where A is a Viper assertion such as method set‘s precondition acc(x.f) && i < x.f. From a caller’s perspective, set‘s pre- and postcondition can be seen as syntactic sugar for appropriate exhale and inhale statements before and after a call to the method.
The informal semantics of exhale A is as follows:
- Assert that all value constraints in
Ahold; if not, verification fails - Assert that all permissions denoted (via accessibility predicates) by
Aare currently held; if not, verification fails - Remove the permissions denoted by
A
The informal semantics of inhale A is as follows:
- Add the permissions denoted by
Ato the program state - Assume that all value constraints in
Ahold
As an example, consider the following Viper program (ignoring, for the moment, the commented-out lines):
field f: Int
method set_inex(x: Ref, i: Int) {
// x.f := i
inhale acc(x.f)
x.f := i
// exhale acc(x.f)
// x.f := i
}
Unlike the previous example, this method has no pre- and postcondition (no requires/ensures). This means that we start verification of the method body in a state with no permissions. The statement inhale acc(x.f) causes the corresponding permission to be added to the state, allowing the assignment on the following line to verify.
- Uncomment the first line of the method body. This will cause a verification error (on that line) since we try to access the location
x.fbefore inhaling the necessary permission. - Alternatively, uncomment the last two lines of the method body. This will cause a verification error for the last line, since we exhale the permission
x.fbefore accessing the heap location. - Uncomment the exhale statement and duplicate it, i.e., attempt to exhale permission to
x.ftwice. What happens?
Self-Framing Assertions
Some Viper expressions and assertions come with conditions under which they are well-defined: e.g., partial operations (such as division) must not be applied outside of their domains (such as 1/n if n is potentially zero).
Well-definedness conditions in Viper guarantee not only that assertions have a meaningful semantics, but that this semantics will be consistent across multiple contexts in which specifications are evaluated. Examples are Viper method specifications and loop invariants: preconditions (postconditions) are evaluated both at the beginning (end) of verifying the method body and before (after) each call to the method; loop invariants are evaluated before and after a loop, as well as at the beginning and end of the loop body.
Such assertions are therefore checked to be guaranteed well-defined in all states they can possibly be evaluated in.
As an example, the assertion n < i/j is not well-defined in general; it cannot be used in e.g. a method precondition unless that precondition also guarantees that the value of j cannot be 0. The assertion j > 0 && n < i/j is well-defined, since the first conjunct is well-defined by itself, and ensures the well-definedness of the second conjunct. In general, the (short-circuiting) order of evaluation of logical connectives is taken into account for well-definedness conditions. For example, j != 0 ==> n < i/j is also well-defined (the right hand side’s value is only used when the left hand side is true, which guarantees its well-definedness condition).
Well-definedness in Viper also requires that all heap locations read by the assertion are accessible, i.e., that the corresponding permissions are held. Again, this must be the case for all possible states in which the assertion could be evaluated.
To ensure this property, Viper requires specification assertions to be self-framing: i.e., each such assertion must include permission to at least the locations it reads. As an example, acc(x.f) and acc(x.f) && x.f > 0 are self-framing, whereas x.f > 0 and acc(x.f.g) are not: in the latter two cases, the meanings of the assertions depend on the value of the field x.f, to which permission is not included.
Viper checks well-definedness, and thus also self-framedness, according to a left-to-right evaluation order. The assertion acc(x.f) && 0 < x.f is therefore accepted as self-framing, but 0 < x.f && acc(x.f) is not. This restriction is typically easy to work around in practice.
The assertions in explicit inhale and exhale statements need not be self-framing because they are evaluated in only one program state; Viper will simply check that the well-definedness conditions for their assertions (e.g., that sufficient permissions are held) are true in that program state.
Exclusive Permissions
Permissions to field locations as described so far are exclusive; it is not possible to hold permission to a location more than once. This built-in principle can indirectly guarantee non-aliasing between references: inhaling the assertions acc(x.f) and acc(y.f) implies x != y because otherwise, the exclusive permission to acc(x.f) would be held twice. This is demonstrated by the following program:
field f: Int
method exclusivity(x: Ref, y: Ref) {
inhale acc(x.f)
inhale acc(y.f)
exhale x != y
}
- Comment one of the two inhale statements. Does the exhale statement still succeed?
- Add the third inhale statement
inhale x == yanywhere before the exhale statement and change the latter toexhale false. Can false be asserted? Why does this demonstrate that it is not possible to hold more than one exclusive permission tox.f?
In Viper, accessibility predicates can be conjoined via &&; the resulting assertion requires the sum of the permissions required by its two conjuncts. Therefore, the two statements inhale acc(x.f); inhale acc(y.f) (semicolons are required in Viper only if statements are on the same line) are equivalent to the single statement inhale acc(x.f) && acc(y.f). In both cases, the obtained permissions imply that x and y cannot be aliases.
Intuitively, the statement inhale acc(x.f) && acc(y.f) can be understood as inhaling permission to acc(x.f), and in addition to that, inhaling the permission to acc(y.f). Technically, this conjunction between resource assertions is strongly related to the separating conjunction from separation logic; formal details of the connection (and how to encode standard separation logic into Viper) can be found in this paper.
We can now see how exclusive permissions enable framing and modular verification, as illustrated by the next example below. Here, method client is able to frame the property b.f == 3 across the call to inc(a, 3) because holding permission to both a.f and b.f implies that a and b cannot be aliases, and because method inc‘s specification states that inc only requires the permission to a.f. Since permission to b.f is retained, the value of b.f can be framed across the method call. Informally, and thinking more operationally, the method would not be able to modify this field location, since it lacks the necessary permission to do so.
field f: Int
method inc(x: Ref, i: Int)
requires acc(x.f)
ensures acc(x.f)
ensures x.f == old(x.f) + i
{
x.f := x.f + i
}
method client(a: Ref, b: Ref) {
inhale acc(a.f) && acc(b.f)
a.f := 1
b.f := 3
inc(a, 3)
assert b.f == 3
}
Note:
- The expression
old(x.f)in methodinc‘s postcondition denotes the value thatx.fhad at the beginning of the method call. In general, an old expressionold(e)causes all heap-dependent subexpressions ofe(in particular, field accesses and calls to heap-dependent functions) to be evaluated in the initial state of the corresponding method call. Note that variables are not heap-dependent; their values are unaffected byold. - Method specifications can contain multiple
requiresandensuresclauses; this has the same meaning as if allrequiresassertions were conjoined, and likewise forensures.
- Add the statement
assert a.f == 4to the end of methodclient; it will verify. Comment the second postcondition ofincto make it fail. What happens if you comment the first (but not the second) postcondition? - Add a method
copyAndInc(x: Ref, y: Ref)with the implementationx.f := y.f + 1. Can you give it a specification such that, when invoked ascopyAndInc(a, b)by methodclientin place of the callinc(a, 3), the statementassert b.f == 3 && a.f == 4in methodclientverifies? - In method
client, change the invocation of methodcopyAndInctocopyAndInc(a, a), and change theassertstatement toassert b.f == 3 && a.f == 2. You’ll probably have to change the specifications of methodcopyAndIncto verify the new code.
Fractional Permissions
Exclusive permissions are too restrictive for some applications. For instance, it is typically safe for multiple threads of a source program to concurrently access the same heap location as long as all accesses are reads. That is, read access can safely be shared. However, if any thread potentially writes to a heap location, no other should typically be allowed to concurrently read it (otherwise, the program has a data race). To support encoding such scenarios, Viper also supports fractional permissions with a permission amount between 0 and 1. Any non-zero permission amount allows read access to the corresponding heap location, but only the exclusive permission (1) allows modifications.
The general form of an accessibility predicate for field permissions is acc(e.f, p), where e is a Ref-typed expression, f is a field name, and p denotes a permission amount. Permission amounts are denoted by write for exclusive permissions, none for zero permission, quotients of two Int-typed expressions i1/i2 to denote a fractional permission; any Perm-typed expression may be used here. Perm is the type of permission amounts, which is a built-in type that can be used like any other type. The permission amount parameter p is optional and defaults to write. For example, acc(e.f), acc(e.f, write) and acc(e.f, 1/1) all have the same meaning.
The next example illustrates the usage of fractional permissions to distinguish between read and write access: there, method copyAndInc requires write permission to x.f, but only read permission (we arbitrarily chose 1/2, but any non-zero fraction would suffice) to y.f.
field f: Int
method copyAndInc(x: Ref, y: Ref)
requires acc(x.f) && acc(y.f, 1/2)
ensures acc(x.f) && acc(y.f, 1/2)
{
x.f := y.f + 1
}
- Change the permission amount for
x.fto9/10, i.e., the corresponding accessibility predicates toacc(x.f, 9/10). Where does the code fail (and why)? - Alternatively, change the implementation to
y.f := x.f + 1. - Revert to the original example. Afterwards, change the permission amount for
y.ftonone(or0/1). Where does the code fail (and why)?
Fractional permissions to the same location are summed up: inhaling acc(x.f, p1) && acc(x.f, p2) is equivalent to inhaling acc(x.f, p1 + p2), and analogously for exhaling. As before, inhaling permissions maintains the invariant that write permission to a location are exclusive. With fractional permission in mind, this can be rephrased as maintaining the invariant that the permission amount to a location never exceeds 1.
To illustrate this, consider the next example (and its exercises): there, the assert statement fails because holding one third permission to each x.f and y.f does not imply that x and y cannot be aliases, since the sum of the individual permission amounts does not exceed 1.
field f: Int
method test(x: Ref, y: Ref) {
inhale acc(x.f, 1/2) && acc(y.f, 1/2)
assert x != y
}
- Change both permission amounts to
2/3. Theassertstatement will now verify. - Revert to the original example. Afterwards, replace the
assertstatement byinhale x == yand add the statementexhale acc(x.f, 1/1)to the end of methodtest. The code verifies, which illustrates that permission amounts are summed up. - Revert to the original example. Afterwards, replace the
assertstatement byexhale acc(x.f, 1/8) && acc(x.f, 1/8), and add the subsequent statementexhale acc(x.f, 1/4). The code verifies, which illustrates that permission amounts can be split up. - Revert to the original example. Afterwards, add a third argument
z: Refto the signature of methodtest, add the conjunctacc(z.f, 1/2)to theinhalestatement and change theassertstatement tox != y || x != z. This verifies , but neither disjunct on their own will. Why?
While fractional permissions no longer always guarantee non-aliasing between references, as demonstrated by the previous example, they still enable framing, e.g., across method calls: from a caller’s perspective, holding on to a non-zero permission amount to a location x.f across a method call guarantees that the value of x.f cannot be affected by the call. That is, because the callee would need to obtain write permission, i.e., permission amount 1, which cannot happen as long as the caller retains its fraction.
The next example illustrates the use of fractional permissions for framing: there, method client can frame the property b.f == 3 across the call to copyAndInc because client retains half the permission to b.f across the call. Note that the postcondition of copyAndInc does not explicitly state that the value of y.f remains unchanged.
field f: Int
method copyAndInc(x: Ref, y: Ref)
requires acc(x.f) && acc(y.f, 1/2)
ensures acc(x.f) && acc(y.f, 1/2)
ensures x.f == y.f + 1
{
x.f := y.f + 1
}
method client(a: Ref, b: Ref) {
inhale acc(a.f) && acc(b.f)
a.f := 1
b.f := 3
copyAndInc(a, b)
assert b.f == 3 && a.f == 4
}
- Add the statement
exhale acc(b.f, 1/2)right before the invocation ofcopyAndInc. Since methodclienttemporarily loses all permission tob.f, the propertyb.f == 3can no longer be framed across the call. Note that methodclientcannot deduce modularly (i.e., without considering the body of methodcopyAndInc) thatcopyAndIncdoes not modifyb.f; the method body might inhale the other half permission (e.g., modelling the acquisition of a lock) and thus, be able to assign tob.f. - Can you fix the new code by changing the specifications of method
copyAndInc? - Revert to the original example. Afterwards, modify method
clientas follows: change the invocation of methodcopyAndInctocopyAndInc(a, a), and change theassertstatement toassert b.f == 3 && a.f == 2. To verify the resulting code, you’ll have to change the specifications of methodcopyAndInc. - Can you find specifications for method
copyAndIncthat allow verifying both versions of methodclient: the original implementation (copyAndInc(a, b); assert b.f == 3 && a.f == 4) and the new one (copyAndInc(a, a); assert b.f == 3 && a.f == 2). That is, can you find specifications that work, regardless of whether or not the passed references are aliases?
Predicates
So far, we have only discussed the specification of programs with a statically-finite number of field locations; our specifications must enumerate all relevant locations in order to express the necessary permissions. However, realistic programs manipulate data structures of unbounded size. Viper supports two main features for specifying unbounded data structures on the heap: predicates and quantified permissions.
Viper predicates are top level declarations, which give a name to a parameterised assertion; a predicate can have any number of parameters, and its body can be any self-framing Viper assertion using only these parameters as variable names. Predicate definitions can be recursive, allowing them to denote permission to and properties of recursive heap structures such as linked lists and trees. Viper predicates may also be declared with no body (in this case, the predicate is abstract), which can be useful for representing assertions whose definitions should be hidden for information hiding reasons, or in more advanced applications of Viper, for adding new kinds of resource assertion to the verification problem at hand.
Predicates are introduced in top-level declarations of the form
predicate P(...) { A }
or
predicate P(...)
where P is a globally-unique predicate name, followed by a possibly-empty list of parameters, and A is the predicate body, that is, an assertion that may include usages of P as well as P‘s parameters. Viper checks that predicate bodies are self-framing. Declarations of the second form (that is, without body) introduce abstract predicates.
A predicate instance is written P(e1,...,en), and is a second kind of resource assertion in Viper: as for field permissions, predicate instances can be inhaled and exhaled (added to and removed from the program state), and the Viper program state includes how many instances of which predicates are currently held.
In Viper, a predicate instance is not directly equivalent to the corresponding instantiation of the predicate’s body, but these two assertions can be explicitly exchanged for one another. The statement unfold P(...) exchanges a predicate instance for its body; fold P(...) performs the inverse operation. Abstract predicates cannot be folded or unfolded.
In the following example, the predicate tuple represents permission to the left and right fields of some tuple (note that this is not a keyword in Viper). The method requires permission to the fields this.left and this.right. Intuitively speaking, the tuple predicate required by the precondition contains permissions to the fields this.left and this.right. Holding the predicate is not enough to be allowed to access these fields; the corresponding permissions, however, can be obtained by unfolding the predicate. On the last line of the method’s body, these permission are folded back into the tuple predicate that is given back to the caller.
field left: Int
field right: Int
predicate tuple(this: Ref) {
acc(this.left) && acc(this.right)
}
method setTuple(this: Ref, l: Int, r: Int)
requires tuple(this)
ensures tuple(this)
{
unfold tuple(this)
this.left := l
this.right := r
fold tuple(this)
}
Viper supports assertions of the form unfolding P(...) in A, which temporarily unfolds the predicate instance P(...) for (only) the evaluation of the assertion A. It is useful in contexts where statements are not allowed such as within method specifications and other assertions. For instance, in the example above we could add a postcondition unfolding tuple(this) in this.left == l && this.right == r to express that the entries of the tuple are set to l and r, respectively.
An unfold operation exchanges a predicate instance for its body; roughly speaking, the predicate instance is exhaled, and its body inhaled. Such an operation causes a verification failure if the predicate instance is not held. A fold operation exchanges a predicate body for a predicate instance; roughly speaking, the body is exhaled, and the instance inhaled. In both cases, however, in contrast to a standard exhale operation, these exhales do not remove information about the locations whose permissions have been exhaled because these permissions are still held, but perhaps folded (or no longer folded) into a predicate.
- In the previous example code above, comment out the
unfoldstatement on the first line ofsetTuple. What fails, and why? What if you instead duplicate this statement? - Try the same with the
foldstatement on the last line of the method body. What fails now? - Add the postcondition
unfolding tuple(this) in this.left == l && this.right == rto the original specification. What happens if you remove theunfolding tuple(this) inpart, and why? - After the
fold tuple(this)statement, add the following lineunfold tuple(this); assert this.left == l; fold tuple(this). Why does this assertion succeed? What if youexhaleand theninhalethe predicate instance before theunfoldyou have just added?
Formally, recursive predicate definitions are interpreted with respect to their least fixpoint interpretations; informally, this implies the built-in assumption that any given predicate instance has a finite (but potentially unbounded) number of predicate instances folded within it. Note that a predicate instance may represent a statically-unknown set of permissions. Holding a predicate instance in a Viper state can be thought of as indirectly holding all of these permissions (though unfolding the predicate will be necessary to make direct use of them).
Analogously to field permissions, it is possible for a program state to hold fractions of predicate instances (unlike for field permissions, these can also be permission amounts larger than 1): this is denoted by accessibility predicates of the shape acc(P(...), p). The simple syntax P(...) has the same meaning as acc(P(...)), which in turn has the same meaning as acc(P(...), write). Folding or unfolding a fraction of a predicate effectively multiplies all permission amounts used for resources in the predicate body by the corresponding fraction. In the example below, one half of a tuple predicate is given to the method. Unfolding this half of the predicate yields half a permission for each of the fields this.left and this.right; which are sufficient permissions to read the fields.
method addTuple(this: Ref) returns (sum: Int)
requires acc(tuple(this), 1/2)
ensures acc(tuple(this), 1/2)
{
unfold acc(tuple(this), 1/2)
sum := this.left + this.right
fold acc(tuple(this), 1/2)
}
The next example is an extract from an encoding of a singly-linked list implementation. The predicate list represents permission to the elem and next fields of all nodes in a null-terminated list. The append method requires an instance of the list predicate for its this parameter and returns this predicate instance to its caller. The body unfolds the predicate in order to get access to the fields of this and folds it back before terminating.
The statement n := new(elem, next) models object creation: it assigns a fresh reference to n and inhales write permission to n.elem and n.next. Notice that unfold list(this) will exchange the predicate instance for its body, which includes the predicate instance list(this.next) if this.next != null. This is important to understand why (when the first branch of the if-condition is taken) two fold statements are needed: one for list(n) and another for list(this): since this.next (or n) is no longer null, folding list(this) depends on first folding list(n).
field elem: Int
field next: Ref
predicate list(this: Ref) {
acc(this.elem) && acc(this.next) &&
(this.next != null ==> list(this.next))
}
method append(this: Ref, e: Int)
requires list(this)
ensures list(this)
{
unfold list(this)
if (this.next == null) {
var n: Ref
n := new(elem, next)
n.elem := e
n.next := null
this.next := n
fold list(n)
} else {
append(this.next, e)
}
fold list(this)
}
- Remove the precondition of
appendand observe that verification fails because the predicate instance to be unfolded (on the first line of the method body) is not held. - Change the predicate definition to require all list elements to be non-negative; change the definition of
appendto maintain this property. - Write a method that creates a cyclic list and attempt to fold the list predicate. Why does this fail? Hint: consider what does the assertion
acc(n.elem) && acc(n.elem)mean in the context of separating conjunction.
It is often useful to declare predicates with several arguments, such as the following list segment predicate, which is commonly used in separation logic. The predicate’s first argument denotes the start of the list segment, the second argument its end (i.e., the node directly after the segment) and the third argument, a value-typed mathematical sequence, represents the values stored in the segment.
field elem : Int
field next : Ref
predicate lseg(first: Ref, last: Ref, values: Seq[Int])
{
first != last ==>
acc(first.elem) && acc(first.next) &&
0 < |values| &&
first.elem == values[0] &&
lseg(first.next, last, values[1..])
}
method removeFirst(first: Ref, last: Ref, values: Seq[Int])
returns (value: Int, second: Ref)
requires lseg(first, last, values)
requires first != last
ensures lseg(second, last, values[1..])
{
unfold lseg(first, last, values)
value := first.elem
second := first.next
}
- Implement a
prependmethod that adds an element at the front of the list. You can useSeq(x) ++ sto concatenate a sequencesto a singleton sequence containingx(see the section on sequences for details). Note that verifying your method will most-likely depend on a sequence identity such as(Seq(x) ++ s)[1..] == s. Such identities are not always provided automatically by the current sequence support. In case your example doesn’t verify, try adding the appropriate equality in anassertstatement; this should tell the verifier to prove the equality first, and then use it. - Write a client method which takes an
lsegin its precondition, calls your prepend method to prepend42to the front, and then usesremoveFirstto get this value back. Can you assert afterwards that the returned value is42? What if you extend the specification ofremoveFirst?
Functions
Just as predicates can be used to define parameterised (and potentially-recursive) assertions, Viper functions define parameterised and potentially-recursive expressions. A function can have any number of parameters, and always returns a single value; evaluation of a Viper function (just as any other Viper expression) is side-effect free. Function applications may occur both in code and in specifications: anywhere that Viper expressions may occur.
Functions are introduced in top-level declarations of the form:
function f(...): T
requires A
ensures E1
{ E2 }
or
function f(...): T
requires A
ensures E1
where f is a globally-unique function name, followed by a possibly-empty list of parameters, and a result type T. Functions may have an arbitrary number of pre- and postconditions; each precondition (indicated by the requires keyword) consists of an assertion A, whereas each postcondition (indicated by the ensures keyword) consists of an expression E1. That is, preconditions may contain resource assertions such as accessibility predicates, but postconditions must not (this difference from methods reflects the fact that function applications are side-effect-free, and so the pre- and post-states of a function application are the same; one can think of function preconditions as also being implicit additional postconditions). The result of the function is referred to using the keyword result in postconditions.
The following example defines a function listLength that takes a null-terminated simply-linked list and computes its length. As shown in the body of listLength, function applications are written simply as the function name followed by appropriately-typed arguments in parentheses. The precondition of listLength expresses the fact that the function application can only be evaluated when the corresponding list predicate instance is held, while the post-condition expresses the fact that the length of a list is always a non-negative integer.
field elem: Int
field next: Ref
predicate list(this: Ref) {
acc(this.elem) && acc(this.next) &&
(this.next != null ==> list(this.next))
}
function listLength(l:Ref) : Int
requires list(l)
ensures result > 0
{
unfolding list(l) in l.next == null ? 1 : 1 + listLength(l.next)
}
The function body declaration { E2 } (if provided) must contain an expression E2 of (return) type T; it may contain function invocations, including recursive invocations of f itself. Function declarations of the latter form (that is, without a function body) introduce abstract functions, which may be useful for information hiding reasons, or to model functions which need not or cannot be directly implemented, e.g., because they model externally-justified information about the encoded program (such as the behaviour of library code). The following example illustrates this by adding a capacity function, intended to model a capacity suitable for storing the elements of the list in an array-like container.
function capacity(l:Ref): Int
requires list(l)
ensures listLength(l) <= result && result <= 2 * listLength(l)
Note that functions declared in Viper domains (i.e. domain functions) are considered by Viper to be abstract state-independent total functions. As such, they can neither have a body nor be equipped with any pre-/postconditions; see the domains section for more details. In contrast, top-level functions can be state-dependent; the ability for function preconditions to include permissions allows them to depend on not only the values of their parameters, but also on heap locations to which their preconditions require permissions.
Viper checks that the function body and any postconditions are framed by the preconditions; that is, the preconditions must require all permissions that are needed to evaluate the function body and the postconditions. Moreover, Viper verifies that the postconditions can be proven to hold for the result of the function. In order to enable function termination checks, which are not performed by default, users can specify termination measures, as discussed in the chapter on termination. As the checking of a recursive function definition is essentially a proof by induction on the unrolling of the definition, not checking termination can lead to unsound behaviour. The following example yields such an inconsistency by means of a non-terminating function:
function bad() : Int
ensures 0 == 1
{ bad() }
Due to the least fixpoint interpretation of predicates, any recursive function whose recursive calls occur inside an unfolding expression are guaranteed to be terminating, as in the case of the listLength function above. Consequently, predicates, and other common well-founded orders, are standard termination measures provided by Viper.
For non-abstract functions, Viper reasons about function applications in terms of the function bodies. That is, in contrast to methods, it is not always necessary to provide a postcondition in order to convey
information to the caller of a function. Nevertheless, postconditions are useful for abstract functions and in situations where the property expressed in the postcondition does not directly follow from unfolding the function body once but, for instance, requires induction. In the case of the listLength function, the non-negativity of the result is indeed an inductive property, and is not exploitable by Viper unless stated in the postcondition.
For every function application, Viper checks that the function precondition is true in the current state, and then assumes the value of the function application to be equal to the function body (if provided), as well as assuming any postconditions. Fully expanding function bodies cannot work for recursive functions. Instead, functions are by-default expanded only once; additional expansions are triggered when unfolding or folding a predicate that is mentioned in the function’s preconditions. This feature allows one to traverse recursive structures and simultaneously reason about the permissions and values. For example, since predicate list was mentioned in the precondition of function listLength earlier, the body of any function call listLength(l) is unfolded whenever a predicate list(l) is. This is why the following implementation of the capacity function can be successfully verified:
function capacity(l:Ref): Int
requires list(l)
ensures listLength(l) <= result && result <= 2 * listLength(l)
{ unfolding list(l) in l.next == null
? 1
: unfolding list(l.next) in l.next.next == null
? 2
: 3 + capacity(l.next.next) }
The example below is an alternative version of the previously shown list segment example from the predicates section: instead of using a predicate parameter for the abstract representation of the list segment (as a mathematical sequence), a function is introduced that computes the abstraction. This usage of functions to eliminate predicate parameters which are redundant (in the sense that their values can instead be computed given any predicate instance and its other parameters) is common in Viper.
field elem: Int
field next: Ref
predicate lseg(this: Ref, last: Ref) {
this != last ==>
acc(this.elem) && acc(this.next) &&
this.next != null &&
lseg(this.next, last)
}
function values(this: Ref, last: Ref): Seq[Int]
requires lseg(this, last)
{
unfolding lseg(this, last) in
this == last
? Seq[Int]()
: Seq(this.elem) ++ values(this.next, last)
}
method removeFirst(this: Ref, last: Ref) returns (first: Int, rest: Ref)
requires lseg(this, last)
requires this != last
ensures lseg(rest, last)
ensures values(rest, last) == old(values(this, last)[1..])
{
unfold lseg(this, last)
first := this.elem
rest := this.next
}
The values function requires an lseg predicate instance in its precondition to obtain the permissions to traverse the list. Its body uses an unfolding expression to obtain the predicate instance required for the recursive application.
- Use the
valuesfunction to strengthen the postcondition ofremoveFirstby stating thatfirstwas indeed the first element of the segment. - Extend the example by a
containsfunction that checks whether or not a list segment contains a given element. - Extend the example by implementing an
appendmethod that appends an element to a list segment (similar to the one used in the predicate section). Afterwards:- Use
containsto express that the appended element is contained in the resulting segment. - Alternatively, use
valuesto express that: (1) the given an element has been appended and (2) that the values stored in the rest of the list segment have not been changed.
- Use
Quantifiers
Viper’s assertions can include forall and exists quantifiers, with the following syntax:
forall [vars] :: [triggers] A
exists [vars] :: e
Here [vars] is a list of comma-separated declarations of variables which are being quantified over, [triggers] consists of a number of so-called trigger expressions in curly braces (explained next), and A (and e) is a Viper assertion (respectively, boolean expression) potentially including the quantified variables. Unlike existential quantifiers, forall quantifiers in Viper may contain resource assertions; this possibility is explained in the section on quantified permissions.
Trigger expressions take a crucial role in guiding the SMT solver towards a quick solution, by restricting the instantiations of a quantified assertion. In particular, when a forall-quantified assertion is a hypothesis for a proof goal, the triggers inform the SMT solver to instantiate the quantifier only when it encounters expressions (which are not themselves under a quantifier) of forms matching the trigger. Let’s first illustrate with an example:
assume forall i: Int, j: Int :: {f(i), g(j)} f(i) && i < j ==> g(j)
assert ...f(h(5))...g(k(7))... // some proof goal
Here, assuming that the SMT solver encounters both the expressions f(h(5)) and g(k(7)), the body of the quantification will be instantiated with i == h(5) and j == k(7), obtaining f(h(5)) && h(5) < k(7) ==> g(k(7)). If no other pairs of expressions matching the triggers are encountered, no other instantiations of the quantifier will be made.
In general, a forall quantifier can have any number of sets of trigger expressions; these are written one after the other, each enclosed within braces. Multiple such sets prescribe alternative triggering conditions; multiple expressions within a single trigger set prescribe that expressions matching each of the trigger expressions must be encountered before an instantiation may be made.
You can check how triggers affect the verification in the following examples:
- in
restrictive_triggersthe triggers are too restrictive and do not allow the right instantiation of the quantifier; - in
dangerous_triggersthe bad choice of the triggers leads to an infinite loop of instantiations (in this case, each instantiation results in a new expression which matches the trigger): a problem known as matching loop. In this case, the SMT solver times out without providing an answer. - in
good_triggersthe choice of the triggers allows the SMT solver to quickly provide the right answer, preventing the problematic matching loop of the previous example.
function magic(i:Int) : Int
method restrictive_triggers()
{
// Our definition of `magic`, with a very restrictive trigger
assume forall i: Int :: { magic(magic(magic(i))) }
magic(magic(i)) == magic(2 * i) + i
// The following should verify. However, the verification fails
// because the triggers are too restrictive and the quantifier
// can not be intantiated.
assert magic(magic(10)) == magic(20) + 10
}
method dangerous_triggers()
{
// Our definition of `magic`, with a matching loop
assume forall i: Int :: { magic(i) }
magic(magic(i)) == magic(2 * i) + i
// The following should fail, because our definition says nothing
// about this equality. However, if you uncomment the assertion
// the verification will time out and give no answer because of the
// matching loop caused by instantiating the quantifier.
// assert magic(magic(10)) == magic(87987978) + 10
}
method good_triggers()
{
// Our definition of `magic`
assume forall i: Int :: { magic(magic(i)) }
magic(magic(i)) == magic(2 * i) + i
// The following verifies, as expected
assert magic(magic(10)) == magic(20) + 10
// The following fails, as expected, because our definition says
// nothing about this equality. The verification terminates
// quickly because we don't have matching loops; the SMT solver
// quickly exhausts the available quantifier instantiations.
assert magic(magic(10)) == magic(87987978) + 10
}
There are a number of restrictions on what can be used as a set of trigger expressions:
- Each quantified variable must occur at least once in a trigger set.
- Each trigger expression must include at least one quantified variable.
- Each trigger expression must have some additional structure (typically a function application); a quantified variable alone cannot be used as a trigger expression.
- Arithmetic and boolean operators may not occur in trigger expressions.
- Accessibility predicates (the
acckeyword) may not be used in trigger expressions.
Applications of both domain and top-level Viper functions can be used in trigger expressions, as can field dereference expressions (e.g. x.f) and Viper’s built-in sequence and set operators. Note that the types of trigger expressions are not restricted; in particular, there is no requirement that trigger expressions are boolean-typed.
If no triggers are specified, Viper will infer them automatically with a heuristics based on the body of the quantifier. In some unfortunate cases this automatic choice will not be good enough and can lead to either incompletenesses (necessary instantiations which are not made) or matching loops; it is recommended to always specify triggers on Viper quantifiers.
The underlying tools currently have limited support for existential quantifications: the syntax for exists does not allow the specification of triggers (which play a dual role for existential quantifiers, in controlling the potential witnesses/instantiations considered when proving an existentially-quantified formula), so existential quantifications should be used sparingly due to the risk of matching loops. This limitation is planned to be lifted in the near future.
For more details on triggers and the e-matching approach to quantifier instantiation, we recommend the Programming with Triggers paper.
Quantified Permissions
Viper provides two main mechanisms for specifying permission to a (potentially unbounded) number of heap locations: recursive predicates and quantified permissions. While predicates can be a natural choice for modelling entire data structures which are traversed in an orderly top-down fashion, quantified permissions enable point-wise specifications, suitable for modelling heap structures which can be traversed in multiple directions, random-access data structures such as arrays, and unordered data structures such as general graphs.
The basic idea is to allow resource assertions such as acc(e.f) to occur within the body of a forall quantifier. In particular, the e receiver expression can be parameterised by the quantified variable, specifying permission to a set of different heap locations: one for each instantiation of the quantifier.
As a simple example, we can model a “binary graph” (in which each node has at most two outgoing edges) in the heap, in terms of a set of nodes, using the following quantified permission assertion: forall n:Ref :: { n.first }{ n.second } n in nodes ==> acc(n.first) && acc(n.second). Such an assertion provides permission to access the first and second fields of all nodes n (as explained in the previous section on quantifiers, the { n.first }{ n.second } syntax denotes triggers). To usefully model a graph, one would typically also require the nodes set to be closed under the graph edges, so that a traversal is known to stay within these permissions; this is illustrated in the following example:
field first : Ref
field second : Ref
method inc(nodes: Set[Ref], x: Ref)
requires forall n:Ref :: { n.first } n in nodes ==>
acc(n.first) &&
(n.first != null ==> n.first in nodes)
requires forall n:Ref :: { n.second } n in nodes ==>
acc(n.second) &&
(n.second != null ==> n.second in nodes)
requires x in nodes
{
var y : Ref
if(x.second != null) {
y := x.second.first // permissions covered by preconditions
}
}
- Remove the second conjunct from the first precondition. The example should still verify. Now change the field access in the method body to be
x.first.first. The example will no longer verify, unless you restore the original precondition. - Try instead making the first precondition
requires forall n:Ref :: n in nodes ==> acc(n.first) && n.first in nodes. The example should verify. Try adding an assert statement immediately after the assignment:assert y != null. This should verify - the modified precondition implicitly guarantees thatn.firstis always non-null (for anyninnodes), since it provides us with permission to a field ofn.first. - Try restoring the original precondition:
requires forall n:Ref :: n in nodes ==> acc(n.first) && (n.first != null ==> n.first in nodes). Theassertstatement that you added in the previous point should no-longer verify, since there is no-longer any reason thatn.firstis guaranteed to be non-null.
Receiver Expressions and Injectivity
In the above examples, the receiver expressions used to specify permissions (the e expression in acc(e.f)) were always the quantified variable itself. This is not a requirement; for example, in the following code, quantified permissions are used along with a function address in the exhale statement, to exhale permission to multiple field locations:
field val : Int
function address(i:Int) : Ref
// ensures forall j:Int, k:Int :: j != k ==> address(j)!=address(k)
method test()
{
inhale acc(address(3).val, 1/2)
inhale acc(address(2).val, 1/2)
inhale acc(address(1).val, 1/2)
exhale forall i:Int :: 1<=i && i<=3 ==> acc(address(i).val, 1/2)
}
The expression address(i) implicitly defines a mapping between instances i of the quantifier and receiver references address(i). Such receiver expressions cannot be fully-general: Viper imposes the restriction that this mapping must be provably injective: for any two instances of such a quantifier, the verifier must be able to prove that the corresponding receiver expressions are different. As usual, this condition can be proven using any information available at the particular program point. In addition, injectivity is only required for instances of the quantifier for which permission is actually required; in the above example, the restriction amounts to showing that the references address(1), address(2) and address(3) are pairwise unequal. In the following exercises, this is illustrated more thoroughly.
- In the above example, try uncommenting the postcondition (
ensuresline) attached to theaddressfunction declaration. The complaint about injectivity should then be removed, since the function postcondition guarantees injectivity ofaddress(i)as a mapping fromito receivers. - Re-comment out the function postcondition (and check that the error re-occurs). In the example code above, try changing the permission amounts from
1/2to1/1throughout. For example, changeacc(address(1).val,1/2)toacc(address(1).val, 1/1)(or toacc(address(1).val), which has the same meaning. This will remove the complaint about injectivity: the permissions held after the threeinhalestatements are sufficient to guarantee the required inequalities. - A further alternative is to add instead an additional assumption (somewhere before the
exhalestatement):inhale address(1) != address(2) && address(2) != address(3) && address(3) != address(1). Again, this should make the verifier happy; as also shown in the previous point, these inequalities are sufficient for theexhaleto satisfy the injectivity restriction; there is no requirement foraddress(i)to be injective in general.
The injectivity restriction imposed by Viper has the consequence that, when considering permissions required via quantified permissions, one can equivalently think about these per instantiation of the quantified variable, or per corresponding instance of the receiver expression.
Magic Wands
Note: this section introduces a somewhat advanced feature of the Viper language, which users who are just starting-out with Viper may wish to skip over for the moment.
When reasoning with unbounded data structures, it can often be useful to specify properties of partial versions of these data structures. For example, during an iterative traversal of a linked list, one typically needs a specification relating the prefix of the list already visited, to a view of the overall data structure. Directly specifying such prefixes (or more generally, instances of data structures with a “hole”), tends to lead to auxiliary predicate definitions (e.g. an lseg predicate for list segments), which in turn necessitate additional lemmas or ghost methods for converting between multiple views of the same structure.
Viper includes a powerful alternative mechanism, which is often useful for evading these problems: the magic wand connective. A magic wand assertion is written A --* B, where A and B are Viper assertions. Like permissions to field locations and instances of predicates, magic wands are a type of resource, instances of which can be held in a Viper program state; these can be added and removed from the state via inhale and exhale operations, just as for other resources.
A magic wand instance A --* B abstractly represents a resource which, if combined with the resources represented by A, can be exchanged for the resources represented by B. For example, A could represent the permissions to the postfix of a linked-list (where we are now), and B could represent the permissions to the entire list; the magic wand then abstractly represents the leftover permissions to the prefix of the list. In this case, both the postfix A and a magic wand A --* B could be given up, to reobtain B, describing the entire list. This “giving up” step, is called applying the magic wand, and is directed in Viper with an apply statement:
inhale A
inhale A --* B
apply A --* B
assert B // succeeds; would fail before the apply statement
To understand a typical use-case for magic wands more concretely, consider the following iterative code for appending two linked lists:
field next : Ref
field val : Int
method append_iterative(l1 : Ref, l2: Ref)
{
if(l1.next == null) { // easy case
l1.next := l2
} else {
var tmp : Ref := l1.next
while(tmp.next != null)
{
tmp := tmp.next
}
tmp.next := l2
}
}
Using a standard linked-list predicate list, and a function elems to fetch the sequence of elements stored in a linked-list, we can specify the intended behaviour of our method, and add a first-attempt at a loop invariant, as follows:
field next : Ref
field val : Int
predicate list(start : Ref)
{
acc(start.val) && acc(start.next) &&
(start.next != null ==> list(start.next))
}
function elems(start: Ref) : Seq[Int]
requires list(start)
{
unfolding list(start) in (
(start.next == null ? Seq(start.val) :
Seq(start.val) ++ elems(start.next) ))
}
method append_iterative(l1 : Ref, l2: Ref)
requires list(l1) && list(l2) && l2 != null
ensures list(l1)
ensures elems(l1) == old(elems(l1) ++ elems(l2))
{
unfold list(l1)
if(l1.next == null) { // easy case
l1.next := l2; fold list(l1)
} else {
var tmp : Ref := l1.next
var index : Int := 1 // extra variable: useful for specification
while(unfolding list(tmp) in tmp.next != null)
invariant index >= 0
invariant list(tmp)
// what about the prefix of the list?
{
unfold list(tmp)
var prev : Ref := tmp // extra variable: useful for specification
tmp := tmp.next
index := index + 1
}
unfold list(tmp)
tmp.next := l2
fold list(tmp)
// how do we get back to list(l1) ?
}
}
In this version of the code, we’ve added the extra variables index (representing how far through the linked-list the tmp reference is), and prev; both will be convenient for writing a specification later in this section. As commented in the file, the specification is not sufficient to verify the code. The loop invariant tracks permission to the postfix linked-list (referenced by tmp). However, it includes neither permissions nor value information about the prefix of the list between l1 and the tmp reference. Since these permissions are not tracked by the loop invariant, they are effectively leaked during the loop execution; with the loop invariant given there is no way after the loop to obtain permission to the entire list (the predicate instance list(l1)), as required in the postcondition.
- Run the example code above. The check of the postcondition should fail, since the required predicate instance
list(l1)is not held after the loop. - Try changing the loop invariant by adding the additional conjunct
&& elems(tmp) == old(elems(l1))[index..]at the end. Re-run the example - the behaviour should be unchanged. This conjunct expresses that the elements fromtmponwards have not been modified so far. - Instead of this additional conjunct, why can’t we simply write
&& elems(tmp) == old(elems(tmp))? You might like to try making this change, and running the example. Recall thatoldexpressions do not affect the evaluation of local variables; the reason is not to do withtmp‘s value directly. Consider instead the precondition ofelems; which predicate instances were held in the pre-state of the method?
We can now employ magic wands to retain the lost permissions. In order to retain (during execution of the loop) the permissions to the previously-visited nodes in the list, we use a magic wand list(tmp) --* list(l1). This magic wand represents sufficient resources to guarantee that if we give up a list(tmp) predicate along with this wand, we can obtain a list(l1) predicate; conceptually, it represents the permissions to the earlier segment of the list between l1 and tmp.
field next : Ref
field val : Int
predicate list(start : Ref)
{
acc(start.val) && acc(start.next) &&
(start.next != null ==> list(start.next))
}
function elems(start: Ref) : Seq[Int]
requires list(start)
{
unfolding list(start) in (
(start.next == null ? Seq(start.val) :
Seq(start.val) ++ elems(start.next) ))
}
method appendit_wand(l1 : Ref, l2: Ref)
requires list(l1) && list(l2) && l2 != null
ensures list(l1) // && elems(l1) == old(elems(l1) ++ elems(l2))
{
unfold list(l1)
if(l1.next == null) { // easy case
l1.next := l2; fold list(l1)
} else {
var tmp : Ref := l1.next
var index : Int := 1
// package the magic wand required in the loop invariant below
package list(tmp) --* list(l1)
{ // show how to get from list(tmp) to list(l1):
fold list(l1) // also requires acc(l1.val) && acc(l1.next)
}
while(unfolding list(tmp) in tmp.next != null)
invariant index >= 0
invariant list(tmp)// && elems(tmp) == old(elems(l1))[index..]
invariant list(tmp) --* list(l1) // magic wand instance
{
unfold list(tmp)
var prev : Ref := tmp
tmp := tmp.next
index := index + 1
package list(tmp) --* list(l1) // package new magic wand
{ // we get from list(tmp) to list(l1) by ...
fold list(prev)
apply list(prev) --* list(l1)
}
}
unfold list(tmp)
tmp.next := l2
fold list(tmp)
apply list(tmp) --* list(l1) // regain predicate for whole list
}
}
The additional loop invariant includes an instance of a magic wand: list(tmp) --* list(l1). Such a magic wand instance denotes a new kind of resource in Viper (in addition to field permissions and predicate instances); as such, it can be inhaled and exhaled just as other resource assertions. This particular magic wand instance can (when applied), be used up to exchange any list(tmp) predicate instance for a list(l1) predicate instance. In this example, the magic wand notionally represents the permissions to the prefix of the list between l1 and tmp. These magic wand instances are created via package operations, which are explained below.
- Run the example code above. The check of the postcondition should succeed, in contrast to the previous example.
- Try changing the loop invariant by adding the additional conjunct
&& elems(tmp) == old(elems(l1))[index..]at the end. Re-run the example - the behaviour should be unchanged. This conjunct expresses that the elements fromtmponwards have not been modified so far. - Instead of this additional conjunct, why can’t we simply write
&& elems(tmp) == old(elems(tmp))? You might like to try making this change, and running the example. Recall thatoldexpressions do not affect the evaluation of local variables; the reason is not to do withtmp‘s value directly. Consider instead the precondition ofelems; which predicate instances were held in the pre-state of the method?
Package operations
There are two ways in which a magic wand instance can be added to the resources held in the program state: they can be inhaled (just as any other Viper resource), or we can instruct Viper to construct a new magic wand instance with a package statement. As an example to explain the feature, we will consider the package before the loop in the code example above. A package statement consists of the keyword followed by the desired magic wand instance (in this case, list(tmp) --* list(l1)), along with an optional block of code delimited by braces. The role of a package statement is to create (and justify the creation of) a new magic wand instance in the following way:
- A subset of the resources held in the current state must be identified as necessary for justifying the new magic wand instance. These must be sufficient resources to ensure that, given the additional resources described in the wand left-hand-side, those on the wand’s right-hand-side can be produced. This set of resources is taken from the current state, and is called the footprint of the newly-created magic wand instance. In our example, these are the field permissions
acc(l1.val) && acc(l1.next)(since, along with the wand’s left-hand-sidelist(tmp), these are sufficient to guarantee the wand’s right-hand-sidelist(l1)). - The
packageoperation must check that, given the selected footprint of resources from the current state, in any heap in which the wand’s left-hand-side assertion is held, the combination of these resources can be exchanged for the wand right-hand-side. Any field locations framed by permissions in the wand’s footprint will be assumed to be unchanged for this check (e.g.l1.next == tmpis known in our example, since permission tol1.nextis in the wand’s footprint). The check is made during thepackageoperation by successively attempting to match the resources required on the right-hand-side with resources provided on the left; if not found on the left-hand-side, the resources must instead be found in the current state (or else thepackageoperation fails with a verification error), and are taken for the wand’s footprint. See our ECOOP’15 paper for more details of how wand footprints are chosen. - It is often the case that the combination of the wand’s left-hand-side and footprint do not directly yield the wand’s right-hand-side, but instead can do so after a number of additional operations are performed. These operations can be specified in the block attached to the
packagestatement. In our example, the wand left-hand-sidelist(tmp)combined with the wand footprintacc(l1.val) && acc(l1.next)are sufficient to guaranteelist(l1)after performing the operationfold list(l1), which is given in the block.
- In the same version of the example above, add a statement
assert acc(l1.next)just before the firstpackagestatement. Run the example; there should be no error. Now try moving yourassertstatement to after thepackageoperation (and its attached block). You should now get an assertion failure; the permission tol1.nexthas been used up in the wand’s footprint. - Try removing the
fold list(l1)statement from the firstpackagestatement. What error do you now get, when running the example?
Heap-dependent expressions
So far, we have used magic wands with only resource assertions on their left- and right-hand-sides. However, in order to prove functional properties about our programs, we will as usual need to employ heap-dependent expressions (e.g. field dereferences and function calls) in our specifications. For example, to prove the postcondition elems(l1) == old(elems(l1) ++ elems(l2)) we need a magic wand which guarantees something about the elements of the lists in our program.
Magic wands can include any Viper assertions and expressions, provided that the left- and right-hand-sides are self-framing assertions. Heap dependent expressions used inside magic wands do not refer to the values in the current heap. Instead, a heap dependent expression on the left of a magic wand refers to the heap when the wand is applied; those on the right-hand-side refer to the heap resulting from the application of the wand.
Recall that the magic wand used so far is list(tmp) --* list(l1). One way to finish our example is to express that the elements that list(l1) will have after applying the magic wand are guaranteed to be a prefix of the elements from the original list, plus whichever elements list(tmp) has at the point of applying the magic wand. Informally, we might consider writing something like elems(l1) == old(elems(l1)[..index]) ++ elems(tmp). However, this expression is not quite well-defined; we never hold both the predicate list(l1) and the predicate list(tmp) at the same time; list(tmp) is given up as part of applying the magic wand itself. In order to evaluate heap-dependent expressions in the state corresponding to the wand’s left-hand-side, Viper supports the construct: old[lhs](e), which may only be used in the right-hand-side of a magic wand, and causes the expression e to be evaluated in the corresponding left-hand state. Thus, we can express our desired magic wand as: list(tmp) --* list(l1) && elems(l1) == old(elems(l1)[..index]) ++ old[lhs](elems(tmp)). The corresponding full version of the example above is presented below:
field next : Ref
field val : Int
predicate list(start : Ref)
{
acc(start.val) && acc(start.next) &&
(start.next != null ==> list(start.next))
}
function elems(start: Ref) : Seq[Int]
requires list(start)
{
unfolding list(start) in (
(start.next == null ? Seq(start.val) :
Seq(start.val) ++ elems(start.next) ))
}
method appendit_wand(l1 : Ref, l2: Ref)
requires list(l1) && list(l2) && l2 != null
ensures list(l1) && elems(l1) == old(elems(l1) ++ elems(l2))
{
unfold list(l1)
if(l1.next == null) {
l1.next := l2
fold list(l1)
} else {
var tmp : Ref := l1.next
var index : Int := 1
package list(tmp) --* list(l1) && elems(l1) == old(elems(l1)[..index]) ++ old[lhs](elems(tmp))
{
fold list(l1)
}
while(unfolding list(tmp) in tmp.next != null)
invariant index >= 0
invariant list(tmp) && elems(tmp) == old(elems(l1))[index..]
invariant list(tmp) --* list(l1) && elems(l1) == old(elems(l1)[..index]) ++ old[lhs](elems(tmp))
{
unfold list(tmp)
var prev : Ref := tmp
tmp := tmp.next
index := index + 1
package list(tmp) --* list(l1) && elems(l1) == old(elems(l1)[..index]) ++ old[lhs](elems(tmp))
{
fold list(prev)
apply list(prev) --* list(l1) && elems(l1) == old(elems(l1)[..index-1]) ++ old[lhs](elems(prev))
}
}
unfold list(tmp)
tmp.next := l2
fold list(tmp)
apply list(tmp) --* list(l1) && elems(l1) == old(elems(l1)[..index]) ++ old[lhs](elems(tmp))
}
}
Statements
This section gives a complete overview of Viper statements. Most of them have been used throughout this tutorial, but we describe them in more detail here.
Assignments
Viper supports the following forms of assignments:
| Statement | Description |
|---|---|
x := e |
Assignment to local variables or result parameters |
e1.f := e2 |
Assignment to heap locations |
x, y := m(...) |
Method calls |
x := new(...) |
Object creation |
Assignments to local variables and result parameters of methods work as
expected. It is not possible to assign to input method parameters. Assignment to heap
locations requires the full permission to the heap location (here,
e1.f). Methods may have any number of result parameters; method call
statements use the appropriate number (and types) of variables on the left-hand side (using the same variable twice on the left-hand side is disallowed).
A
method call can be understood as an exhale of the method precondition, a reassignment of the variables used to store result parameters, and inhale of the method postcondition.
Finally, a new statement creates a new object and inhales exclusive permission
to all (possibly none) fields listed comma-separated within the parentheses. As a special case, x := new(*) inhales permission to
all fields declared in the Viper program. Note that neither method calls nor
object creation are expressions. Hence, they must not occur as receivers, method
arguments, etc.; instead of nesting these constructs, one typically assigns their results first to local variables, and then uses these.
Control Structures
Viper supports two main control structures: conditional statements and loops. Conditional statements have the following form:
if(E) {
S1
} else {
S2
}
where the else branch is optional. The semantics is as expected.
Loops have the following form:
while(b)
invariant A
{
S
}
Loops are verified as follows: with respect to the scope surrounding the loop, verification amounts to replacing the loop with the following operations:
Exhale the loop invariant;
Havoc (assign arbitrary values) to all locals and result parameters that get assigned to by the loop body
S(the so-called loop targets);Inhale the loop invariant and the negation of the loop condition
b; the verification of any code following the loop proceeds from this state.
Note that this approach provides two forms of framing: first, locals and result parameters that are not loop targets are always known to be unchanged by the loop. Second, the value of those heap locations for which the context of the loop holds some permission that is not transferred into the loop via the loop invariant are also known to be unchanged. Consequently, it is not necessary to write explicit loop invariants to preserve information about these variables and locations, as is illustrated by the following example:
field f: Int
field g: Int
method Foo(this: Ref, n: Int)
requires acc(this.f) && acc(this.g)
{
var i: Int := n
var x: Int := 3
this.f := 5
while(0 <= i)
invariant acc(this.g)
{
this.g := this.g + 1
i := i - 1
}
assert this.f == 5
assert x == 3
}
- Strengthen the loop invariant to include exclusive permission to
this.f. The firstassertstatement will now fail to verify because the value ofthis.fis no longer framed around the loop - Adapt the loop invariant such that the
assertstatement verifies again. You could use fractional permissions or introduce an additional local variable to remember the value ofthis.f - Add an assignment
x := 3in the loop body. The secondassertstatement will now fail to verify becausexis now a loop target and, thus, its value is no longer framed around the loop - Strengthen the loop invariant such that the
assertstatement verifies again.
The loop body is verified starting from a state that contains no permissions and in which all loop targets have arbitrary values (all other variables in scope will be known to have the same values as they did immediately before the loop). Verification of the loop body then proceeds as follows:
Inhale the loop invariant and the loop condition
b;Verify the loop body
S;Exhale the loop invariant.
Analogous to functions, Viper does also not check loop (or method) termination per default, see the chapter on termination for more details. Alternatively, custom termination checks can be encoded through suitable assertions (see the labelled old expressions described in the section on expressions).
Assertion Checking
| Statement | Description |
|---|---|
exhale A |
Check value properties and remove permissions |
inhale A |
Add permissions and assume value properties |
assert A |
Check permissions and value properties |
assume A |
Assume permissions and value properties |
refute A |
Refute permissions and value properties |
exhale Aandinhale Aare explained in the section on permissions.assert Ais similar toexhale A, but it does not remove any permissions.assume Ais similar toinhale A, but it does not add any permissions.refute Atries to show thatAholds for all executions that reach the statement, and causes a verification error if this is the case. In other words, ifAis provable in some, but not all, execution paths, then the statement still passes.
Note that inhale acc(...) adds the given permission to the current state, whereas assume acc(...) only keeps executing if the given permission was already in the current state.
Verifier Directives
| Statement | Description |
|---|---|
unfold P(...) |
Unfold a predicate instance |
unfold acc(P(...),p) |
Unfold p amount of a predicate instance |
fold P(...) |
Fold a predicate instance |
fold acc(P(...),p) |
Fold p amount of a predicate instance |
package A1 --* A2 |
Create a magic wand instance |
apply A1 --* A2 |
Apply a magic wand instance |
unfoldandfoldare explained in the section on predicatespackageandapplyare explained in the section on magic wands- Note that
unfoldingis an expression, not a statement
Expressions and Assertions
Expressions
Viper supports a number of different kinds of expressions, which can be evaluated to a value of one of the types supported in Viper.
The primitive types supported in Viper are booleans (Bool), integers (Int), permission amounts (Perm), denoting real numbers, and references to heap objects (Ref). In addition, there are built-in parameterised set (Set[T]), multiset (Multiset[T]), sequence (Seq[T]), and map (Map[T, U]) types, and users can define custom types using domains.
Evaluating an expression never changes the state of the program, i.e., expression evaluation has no side effects. However, expression evaluation comes with well-definedness conditions for some expressions: evaluating an expression can cause a verification failure if the expression is not well-defined in the current program state; this leads to a verification error. As an example, the expression x % y is not well-defined if y is equal to zero, and the expression o.f is only well-defined if the current method has the permission to read o.f (which also implies that o is not null).
In the following, we list the different kinds of expressions, remark on their well-definedness conditions (if any) and the value that they evaluate to.
Expressions of multiple types
field access
e.f: to be well-defined, this requires at least some permission to read the field location; returns a value of the type of the field.function application
f(...): the function can either be a domain function or a top-level, (potentially heap-dependent) function. In the latter case, for a function application to be well-defined the function’s precondition must be fulfilled, and in both cases, the argument expressions must be well-defined and have the expected types. Evaluates to a value of the return type of the function. See the respective sections for more information on top-level functions and domains.typed function application
(f(...) : Type): a variant of the above that additionally enforces that the return type of the function application to be the one given in the expression. This is particularly useful with domains with type parameters, for example(Nil() : List[Bool]). The parentheses are mandatory.local variable and parameter evaluation
x: read the current value of the named variable or parameter. Note that it is possible to read local variables which have not been assigned to; in this case, the expression will evaluate to an arbitrary value of its type.conditional expressions
e1 ? e2 : e3, wheree1has typeBoolande2ande3must have the same type; evaluates toe2ife1istrue, and otherwise toe3. Short-circuiting evaluation is taken into account when checking well-definedness conditions; e.g.e2need only be well-defined whene1evaluates to true.unfolding expressions
unfolding acc(P(...), p) in e: Requires that the current method has at least the permission amountpof the predicate instanceP(...). Evaluatesein a context where (this amount of) the predicate instance has been temporarily unfolded (i.e.,Pis no longer available, but its contents are).old and labelled-old expressions
old(e)andold[l](e): Evaluates expressionein a different (older) version of the heap. In the first case, this is the heap at the start of the current method call; in the second, it is the heap at the position of the labell. For the second expression to be well-defined, the labellmust be in the same method as the old-expression, and must have been encountered by the time the old-expression is evaluated; as a result, old-expressions cannot be used in functions, predicates or preconditions (they also cannot be used in postconditions but for a different reason: they would be meaningless for the caller). It is not supported to refer back to a label inside a loop body from outside of the loop body. Note that old expressions does not affect the value of variable references;old(x.f), for example, evaluates to the value that the fieldfof the object that the variablexcurrently points to had at the beginning of the method.function results
result: Can only be used in postconditions of top-level Viper functions, and refers to the result of the function application; it therefore has the type of the return value of the function the postcondition belongs to.let expressions
let v == (e1) in e2: Evaluatese1, and subsequently evaluatese2in a context where the variablevis bound to the value ofe1(currently, the parentheses are necessary). Let expressions are often convenient when one needs to write an expression with many repetitions, or one that concerns several different heaps. For example, if one wishes to evaluate the argument of a function callf(x.f)in the current state and the function application itself in the current method’s old state, this can be expressed by using a let expression as follows:let y == (x.f) in old(f(y)).
Integer expressions
constants, e.g.
-2,1023123909. Integers in Viper are signed and unbounded.unary minus
-e: Negates the value ofeifeis itself an integer.addition, subtraction, multiplication, division, modulo (
e1 + e2,e1 - e2,e1 * e2,e1 / e2,e1 % e2). For all of these, both operands are expected to be integers, and the result will be an integer. These operators are overloaded; similar operators exist returningPerm-typed values; Viper will choose the appropriate operator based on the type information available. The only observable ambiguity is for division, since integer division truncates andPerm-typed division does not. In ambiguous cases, the alternative syntaxe1 \ e2can be used to forceInt-typed division (Perm-typed is otherwise the default).
Boolean expressions
constants
trueandfalseconjunction
e1 && e2, disjunctione1 || e2, implicatione1 ==> e2. For all cases, both operands are expected to be booleans, and the result will be a boolean. Viper has short-circuiting semantics for these operators, meaning that, for example, ine1 && e2,e2will only be evaluated ife1evaluates totrue. In particular, this means thate2only has to be well-defined ife1is true.equality
e1 == e2and inequalitye1 != e2on all types. Both operands have to be of the same type, and the result is a boolean.quantifiers
forallandexists. See the section on quantifiers for more details.For-perm quantifiers
forperm x: Ref [x.f] :: e. This expression serves as a quantifier over all objects for which a permission to the specified field is held by the current method. Inside the expressionein the body, the variablexpoints to an object for which a positive amount of permission tox.fis held. The entire expression is true ifeis true for every such object, and false otherwise. As an example,forperm x: Ref [x.g] :: x.g > 0is true if and only if, for all objects to whoseg-fields the current method holds a permission, the value of theg-field is positive.
forperm expressions are useful for implementing leak checks. For example, by asserting forperm x: Ref [x.f] :: false we can check that in the current context we do not hold any permission to the field f. Note that forperm expressions are evaluated in the current heap, including side-effects caused during exhale operations, as illustrated in the following example:
inhale acc(x.f)
exhale forperm x: Ref [x.f] :: false // Would fail because we have acc(x.f)
acc(x.f) && forperm x: Ref [x.f] :: false // Would succeed because we do not have acc(x.f) anymore.
This is useful, for example, for checking that after the method postcondition is exhaled, the method body does not have any permission left which would be leaked.
Forperm expressions may not be used in functions or predicates.
equivalence or bi-implication
e1 <==> e2, where both expressions are of typeBool, is equivalent to writinge1 == e2.negation
!e: Negates the boolean expressione.integer or perm comparisons
e1 < e2,e1 <= e2,e1 > e2,e1 >= e2require that the operands are either both of typeIntor both of typePerm, and return aBool.
Set and multiset expressions
Viper has a built-in parametric finite set type Set[T], where T is a type parameter that describes the type of the elements of the set. Sets are immutable (i.e. represent mathematical sets).
empty set:
Set[T]()returns an empty set of typeSet[T]. The type argumentTis optional if the type is clear from the context; then simplySet()can be written.set literals:
Set(e1, e2, ..., en)evaluates to a set containing only the n enumerated values and has the typeSet[T], whereTis the common type of the enumerated expressions.e1 union e2,e1 intersection e2,e1 setminus e2perform the respective set operations. In all cases,e1ande2must be sets of the same type, and the entire expression has the same type as its operands. These operators each define a set; the operand sets will not be modified (Viper sets are immutable).e1 subset e2has typeBooland evaluates totrueif and only ife1is a subset ofe2. Again, both operands have to be sets of the same type.Similarly,
e1 in e2, wheree2has the typeSet[T]for someTande1has typeT, evaluates to true if and onlye1is a member ofe2.set cardinality
|s|evaluates to a non-negative integer that represents the cardinality ofs.
Similar to sets, Viper supports multisets:
Literals can either be empty multisets (
Multiset[T]()) or non-empty ones (Multiset(e, ...)) and work like their set counterparts.As for sets, the operations
union,intersection,setminus,subsetand cardinality|s|are supported.e1 in e2, wheree1has typeTande2has typeMultiset[T], denotes the multiplicity ofe1ine2.
Sequence expressions
Viper’s built-in sequence type Seq[T] represents immutable finite sequences of elements of type T.
empty sequence:
Seq[T]()evaluates to an empty sequence of typeSeq[T]. As with empty set literals, the type argument only has to be stated explicitly if it is not clear from the surrounding context.sequence literal:
Seq(e1, e2, ..., en), wheree1-enare expressions that all have a common typeT, represents a sequence of typeSeq[T]ofnelements, whose elements are the argument expressions (i.e., the first element ise1, the seconde2etc., and the last isen.integer sequence literals:
[e1..e2], wheree1ande2areInt-typed, represent the sequence of integers ranging frome1until, but excluding,e2(or the empty sequence, ife2is less than or equal toe1).sequence lookup:
s[e], wheresis an expression of typeSeq[T]for someTandeis an integer, returns the element at indexein the sequence. As a well-definedness condition,emust be known to be non-negative and less than the length ofs, otherwise this expression will result in a verification error.sequence concatenation:
e1 ++ e2results in a new sequence whose elements are the elements ofe1, followed by those ofe2.sequence update:
s[e1 := e2], wheree1has typeInt,shas typeSeq[T]for someTande2is of typeT, denotes the sequence that is identical tos, except that the element at indexe1ise2(the operation does not change the original sequence’s value, but rather defines a new sequence).sub-sequence operations:
s[e1..e2], wheresis a sequence ande1ande2are integers, returns a new sequence that contains the elements ofsstarting from indexe1until (but not including) indexe2. The values ofe1ande2need not be valid indices for the sequence; for negativee1the operator behaves as ife1were equal to0, fore1larger than|s|the empty sequence will result (and vice versa fore2). Optionally, either the first or the second index can be left out (leading to expressions of the forms[..e]ands[e..]), in which case only elements at the end or at the beginning ofsare dropped, respectively.sequence length:
|s|returns the length of a sequence as an integer.sequence member check:
e in sevaluates to true ifeis in the sequences.
Map expressions
Viper has a built-in parametric partial map type Map[K, V], where K is a type parameter that describes the type of the keys in the map, and V similarly describes the type of the values in the map. Like sets, maps are immutable (i.e., they represent mathematical maps), and they map a finite amount of keys to values.
empty map:
Map[K, V]()returns an empty map of typeMap[K, V], i.e., a map whose domain is empty. As with empty set literals, the type arguments are optional if the type is clear from the context; then simplyMap()can be written.map literals:
Map(e1 := e2, e3 := e4, ...)evaluates to a map containing only the explicitly enumerated mappings (i.e, mapping e1 to e2, e3 to e4 etc.), where all keys must have a common typeKand all values must have a common typeVs.t. the resulting expression has the typeMap[K, V]. If multiple key-value pairs have the same key, the map contains the value of the latest such pair. I.e.,Map(1 := 3, 1 := 5)will contain value 5 for key 1.map domain and range: If
mis a map of typeMap[K, V], thendomain(m)is the finite domain (of typeSet[K]) ofm, i.e., the set of keys it contains. Similarly,range(m)denotes the range (or image) ofm, which has typeSet[V].map cardinality:
|m|denotes the cardinality of the mapm, i.e., the cardinality of its domain.map lookup: If
mis a map of typeMap[K, V]andehas a typeK, thenm[e]looks up the value of keyeinm. As a well-definedness condition,emust be known to be in the domain ofm, otherwise this expression will result in a verification error.map membership:
e in m, wheremhas typeMap[K, V]andehas typeK, is true iffeis in the domain ofm.map update: If
mis a map of typeMap[K, V],e1has typeKande2has typeV, thenm[e1 := e2]is a map that is identical tomexcept the key-value-paire1 -> e2has been added (or its value updated).
Perm expressions
Expressions of type Perm are real numbers and are usually used to represent permission amounts (though they can be used for other purposes).
Fractional permission expressions
e1/e2, where bothe1ande2are integers, evaluate to a Perm value whose numerator ise1and whose denominator ise2. A well-definedness condition is thate2must not equal 0.e1/e2can also denote a permission amount divided by an integer ife1is an expression of typePermande2is an expression of typeInt.The
Perm-typed literalsnoneandwritedenote no permission and a full permission, corresponding to0/1and1/1, respectively.The special literal
wildcarddenotes an unspecified positive amount. The specific value represented bywildcardis not fixed but is chosen anew every time awildcardexpression is encountered. In particular, if awildcardamount of permission to a field or predicate is to be exhaled, a value less than the currently held amount is chosen, so that it is always possible to exhale (or assert having) awildcardamount of any permission, unless no permission at all is currently held. However, exhaling and subsequently inhaling awildcardpermission to a location will not restore the initial permission amount, since it will not be known that the inhaledwildcardamount is equal to the exhaled one. Thewildcardpermission amount provides a convenient way to implement duplicable read-only resources, which, for example, can be used to model immutable data.perm(e.f): Evaluates to the amount of permission the current method has to the specified location. Similarly,perm(P(e1, ..., en))returns the amount of permission held for the specified predicate instance. Similarly toforperm, the values ofpermexpressions take into account the side-effects of e.g. ongoingexhaleoperations. For exampleexhale acc(x.f) && perm(x.f) > noneshould always fail, whileexhale perm(x.f) > none && acc(x.f)will succeed (if the full permission tox.fwas held before theexhale).Permissions can be added (
e1 + e2), subtracted (e1 - e2), multiplied (e1 * e2) or divided (e1 / e2). In the first two cases,e1ande2must both bePerm-typed. In the case of multiplication, either twoPerm-typed expressions or onePerm-typed and oneInt-typed are possible. For divisions, the first expression must bePerm-typed and the second of typeInt(though of course ordinary fractions, where both expressions areInt-typed, also exist). The results in all cases will bePerm-typed expressions.
Reference expressions
Reference-typed expressions denote either objects or the special value null (denoted by the null literal). The most important fact about null is the built-in assertion that permissions to fields of null cannot exist; Viper will deduce from holding a field permission that the receiver of the field location is non-null. The analogous assumption does not hold e.g. for predicate instances; it is possible for null to be the value of a predicate parameter.
Assertions
In addition to expressions, Viper supports three kinds of resource assertions: accessibility predicates for fields, predicate instances, and magic wands.
boolean expressions: any boolean expression can also be used as an assertion. This includes disjunctions; note, however, that Viper does not support disjunctions whose disjuncts contain resource assertions (such as accessibility predicates). If such a disjunction is desired where at least one of the operands is a pure expression, this can be rewritten as a conditional expression.
Field permissions are denoted by accessibility predicates
acc(e.f)andacc(e.f, p), whereeis an expression of typeRef,fis a field in the program, andpis an expression of typePerm, denotes a permission amount ofpto the fielde.v. The former is equivalent to writingacc(e.f, write).Predicate instances can be denoted by
acc(P(...))andacc(P(...), p)(the latter denotes a permission amountpof a predicate instanceP(...)). Where the amount iswrite, the simpler syntaxP(...)can also be used.Magic wands
A1 --* A2represent the permission to get assertionA2in exchange for giving up assertionA1.Conjunctions
A1 && A2(similar to the separating conjunction*in separation logic); see the section on fractional permissions.Implication
b ==> A, denotes that assertionAholds if the boolean expressionbis true. Note that only pure expressions may occur on the left of implications, not general assertions.Quantified assertions
forall x: T :: A, whereAis a Viper assertion potentially containing resource assertions, such as accessibility predicatesacc(e.f, p).Conditional assertions
e ? A1 : A2denote thatA1holds if the (pure) boolean expressioneis true, and otherwiseA2holds.Inhale-exhale assertions
[A1, A2]behave likeA1when they are inhaled, but likeA2when they are exhaled. As an example,inhale [acc(x.f), acc(x.g)]is equivalent toinhale acc(x.f). On the other hand, the assertion[acc(x.f), acc(x.g)]in a method precondition means that when calling the method, the caller has to give up (exhale) a permission tox.g, but when verifying the method body, the verifier inhales permission tox.fat the beginning.
Domains
Domains enable the definition of additional types, mathematical functions, and axioms that provide their properties. Syntactically, domains consist of a name (for the newly-introduced type), and a block in which a number of function declarations and axioms can be introduced. The following example shows a simple domain declaration:
domain MyDomain {
function foo(): Int
function bar(x: Bool): Bool
axiom axFoo { foo() > 0 }
axiom axBar { bar(true) }
axiom axFoobar { bar(false) ==> foo() == 3 }
}
The functions declared in a domain are global: one can apply them in any other scope of the Viper program. Functions declared inside a domain are called domain functions; these are more restricted than the standard Viper functions described previously. In particular, domain functions cannot have preconditions; they can be applied in any state. They are also always abstract, i.e., cannot have a defined body. The typical way to attach any meaning to these otherwise-uninterpreted functions, is via domain axioms.
Domain axioms are also global: they define properties of the program which are assumed to hold in all states. Since there is no restriction on the states to which an axiom applies, it must be well-defined in all states; for this reason, domain axioms cannot refer to the values of heap locations, nor to permission amounts (e.g., via perm expressions). In practice, domain axioms are standard (often quantified) first-order logic assertions. Axiom names are used only for readability of the code, but are currently not optional.
domain Neg {
function not(cond: Bool): Bool
}
method TestNeg() {
}
Consider the code snippet above.
Add an axiom
ax_Negexpressing that the functionnotnegates the conditioncond.i. Write the axiom using a universal quantifier.
ii. Write the axiom without using quantifiers.
Hint: Typically, domain axioms require quantifiers, as the domain (in the mathematical sense) of most domain functions is unbounded.
Fill in the body of method
TestNegwith an assertion that tests the behavior ofnot. (Hint: write an assertion that checks the following query for an arbitrary Boolean valuex:not(not(x)) == x).
In the remainder of this section, we will illustrate some use-cases of domains for defining additional types and concepts within a Viper program.
Declaring New Types
The following domain defines a new type MyType with two type parameters:
domain MyType[A,B] {
function constructor_a(x: A): MyType[A,B]
function constructor_b(y: B): MyType[A,B]
function bin_oper(a: MyType[A,B], b: MyType[A,B]): MyType[A,B]
}
In this demo we create a new type called MyType. It’s defined with two type parameters A and B. The encoding provides two constructors and a binary operation.
The following client code demonstrates how the type MyType can be used in a Viper program:
method client(a: MyType[Bool, Ref])
requires a == bin_oper(a,a)
{
var b: MyType[Int, Bool] := constructor_a(11)
var c: MyType[Int, Bool] := constructor_b(true)
var d: MyType[Int, Bool] := bin_oper(b,c)
// The following code will be rejected by the typechecker,
// because a and d are created with different type parameters.
var e: MyType[Int, Bool] := bin_oper(a,d)
}
Note that Viper does not support type parameters as part of function and method declarations; the only type parameters available are those of the enclosing domain. This has the practical implication that one must instantiate all type parameters of a domain type before they can be used outside of the domain definition. This instantiation is usually implicit; so long as the type-checker can figure out the necessary instantiations, then they need not be provided.
By default, Viper provides only two built-in operations for domain types: == and !=. Other operations must be encoded via domain functions and given a meaning via appropriate domain axioms.
Encoding a list ADT
For a more realistic demo, we can encode an algebraic list datatype. We start with the function declarations.
domain List[T] {
/* Constructors */
function Nil(): List[T]
function Cons(head: T, tail: List[T]): List[T]
/* Destructors */
function head_Cons(xs: List[T]): T // requires is_Cons(xs)
function tail_Cons(xs: List[T]): List[T] // requires is_Cons(xs)
/* Constructor types */
function type(xs: List[T]): Int
unique function type_Nil(): Int
unique function type_Cons(): Int
/* Axioms omitted */
}
A mathematical list needs two constructors: Nil, which takes no parameters, and Cons, which takes a scalar value of type T and the tail list (of type List[T]) and returns the new list.
An algebraic datatype requires a deconstructor for each parameter of each of its constructors (alternatively, if one implements tuple types, one can write a single destructor for each constructor). In the case of a list ADT, we will need only two deconstructors (for the parameters of Cons). The deconstructors are called head_Cons and tail_Cons, respectively.
Finally, we encode the integer function type which denotes whether the type of the list constructor is Nil or Cons. In this case, we could use a Boolean function for this purpose. However, there could be more than two constructors of an ADT in the general case.
Notice that we use the keyword unique to declare domain functions whose values (while not concretely known) should be guaranteed different from those returned by any other unique domain functions. Sometimes the value of a function is irrelevant by itself, as long as it is guaranteed to be unique, as in the case of identification functions type_Nil and type_Cons.
The full axiomatisation of these functions and some use cases are available in the Encoding ADTs example.
Axiomatising Custom Theories
Custom axioms can specify the semantics of mathematical functions. Functions typically have parameters, hence the corresponding axioms usually have a universal quantification over a range of possible values as arguments.
domain MyInteger {
function create_int(x: Int): MyInteger
function get_value(a: MyInteger): Int
function sum(a: MyInteger, b: MyInteger): MyInteger
axiom axSum {
forall a: MyInteger, b: MyInteger ::
sum(a,b) == create_int( get_value(a) + get_value(b) )
}
}
Triggers
The axiom axSum uses a universal quantifier (forall) to express the value of sum(a,b) for arbitrary values of the arguments a and b, respectively. In order to apply this axiom, the SMT-solver must instantiate the quantified variables with concrete values in a given context. So, as explained in the section on quantifiers, it is highly important to choose good triggers for the quantifier to avoid performance issues during the verification. Poorly selected triggers may as well disallow the instantiation of the quantifier in cases in which the instantiation is needed.
In the example above, one would intuitively expect the axiom axSum to be applied whenever the function sum is applied to some pair of arguments. Therefore, it makes sense to specify { sum(a,b) } as the trigger, as in the example below:
domain MyInteger {
function create_int(x: Int): MyInteger
function get_value(a: MyInteger): Int
function sum(a: MyInteger, b: MyInteger): MyInteger
axiom axSum {
forall a: MyInteger, b: MyInteger :: { sum(a,b) }
sum(a,b) == create_int( get_value(a) + get_value(b) )
}
}
Recall that a proper trigger must mention all quantified variables.
If the trigger is omitted, the Viper tools attempt to infer possible triggers based on the body of the quantifier. However, this can result in unreliable behavior in general; it is highly recommended to write triggers for all quantifiers in a Viper program. For example, if we remove the explicit trigger from the case above, any of the following triggering terms could be inferred:
{ sum(a,b) }{ get_value(a), get_value(b) }{ sum(a,b) }{ get_value(a), get_value(b) }{ get_value(a), get_value(b) }{ sum(a,b) }
Recall that, for example, create_int( get_value(a) + get_value(b) ) is not a valid trigger, because it contains the arithmetic operator +.
Sometimes it is beneficial to choose expressions as triggers which are not present in the body of the quantifier. For instance, this can help avoiding matching loops.
Axiom-Caused Unsoundness
Just as with any other kind of assumption in a Viper program, one can introduce unsoundness by adding domain axioms. For the simplest case, consider the following example:
domain Foo {
axiom Unsound {
false
}
}
method smokeTest()
{
assert false // verifies
}
Viper is able to verify this program, because the axiom Unsound is assumed to be true in all states of the program, including those in the body of method test. While unsoundnesses in user-defined axioms can be much more subtle than in this example, the simple strategy of checking that one cannot assert false at various program points is often effective for catching basic mistakes, especially if some other surprising verification result has already been observed.
domain MyInteger {
// copied from above without modification
function create_int(x: Int): MyInteger
function get_value(a: MyInteger): Int
function sum(a: MyInteger, b: MyInteger): MyInteger
axiom axSum {
forall a: MyInteger, b: MyInteger :: { sum(a,b) }
sum(a,b) == create_int( get_value(a) + get_value(b) )
}
}
method test1(a: MyInteger, b: MyInteger)
{
assert get_value(a) + get_value(b) == get_value(sum(a, b))
}
method test2(i: Int, j:Int)
{
assert sum(create_int(i), create_int(j)) == create_int(i + j)
}
Consider the two test cases above for the previously-declared datatype
MyInteger. Observe that these tests do not verify with just the one axiomaxSum.Write an additional axiom that fixes the problem.
i. Try manually instantiating
axSumfor one of the tests.ii. What is the missing step in the reasoning that cannot be done without adding an additional axiom?
Hint: One may view the
MyIntegerdatatype as a simple ADT, which means that there exists a bijection betweenIntandMyInteger.iii. What is the right trigger for your axiom? Make sure that, together with your new axiom,
test1andtest2verify.iv. Add an
assert falseat the end of each of the methods, to check that your axiom has not introduced any clear unsoundness.Can you think of any other axioms that can be added to the domain in order to define
MyIntegermore completely? (Hint: does your axiom from the last step express a bijection or an injection?)
Encoding an Array Datatype
We proceed next with an example encoding of integer arrays. Note that arrays are not built-in in Viper, so we have to model an array type. Since array locations should be on the heap, we do this with a combination of a domain, a field, and quantified permissions. Let’s first consider a suitable domain:
domain IArray {
function slot(a: IArray, i: Int): Ref
function len(a: IArray): Int
function first(r: Ref): IArray
function second(r: Ref): Int
axiom all_diff {
forall a: IArray, i: Int :: { slot(a,i) }
first(slot(a,i)) == a && second(slot(a,i)) == i
}
axiom len_nonneg {
forall a: IArray :: { len(a) }
len(a) >= 0
}
}
The idea behind this encoding is to use a Viper object with a single field to model each element of an array. The slot function plays the role of mapping an array and integer index to the corresponding object. We express that the slot function is an injective mapping via the axiom all_diff. The two functions first and second together play the role of an inverse to the slot(a,i) function.
Intuitively, this axiom expresses that for any pair (a, i), slot(a,i) defines a unique object (which will provide the memory location for the array slot).
In addition, we encode the function len for specifying the length of an array, and the axiom len_nonneg which expresses that this function never returns a negative value.
Because the elements of the array will be located on the heap, we need a way of specifying permissions to a range of array elements. We can use quantified permissions for this, and create the following macro definition for specifying permissions to the whole array:
field val: Int
define access(a)
(forall j: Int :: 0 <= j && j < len(a) ==> acc(slot(a,j).val))
Note that, in Viper, we cannot refer to a specific program state from within domains. In particular, we cannot mention slot(a,j).val inside the axioms of IArray, since its meaning depends on a particular heap, and its well-definedness condition depends on whether one holds the appropriate permissions. The state-dependent part of the array encoding is taken care of outside of this domain. In particular, we can now use access in the following client code:
method client()
{
// Create an integer array with three elements
var a: IArray
inhale len(a) == 3
inhale access(a) // access to all array slots
// Initialize the elements of an array
var i: Int := 0
while ( i < len(a) )
invariant 0 <= i && i <= len(a)
{
slot(a,i).val := -i // models a[i] := -i
i := i + 1
}
}
This method will not verify without adding a suitable loop invariant. If we still try, Viper will report the following message:
Assignment might fail. There might be insufficient permission to access slot(a, i).val.
Therefore, we need to add the permissions to the array to the loop invariant:
invariant access(a)
For a complete example, see the Viper encoding of Array Max, by elimination.
ADT plugin
adt List[T] {
Nil()
Cons(value: T, tail: List[T])
}
The ADT plugin is an extension to Viper that enables declarations of algebraic datatypes. These consist of one or more constructors, each of which has zero or more arguments. Any instance of such a datatype then corresponds to exactly one of these constructors. There is syntax to identify which constructor an instance corresponds to, as well as syntax to extract the arguments given to that constructor. As in the example above, ADTs can have type parameters and can be recursive.
Internally, the ADT syntax is translated into domains and domain function applications.
The plugin is enabled by default, and can be disabled with the command-line option --disableAdtPlugin.
Discriminators
For every constructor of the ADT, a discriminator is generated. Syntactically, this is a field with the name is<Constructor> with a Bool type.
assert Cons(1, Cons(2, Nil())).isCons
assert Nil().isNil
Destructors
For every argument of every constructor of the ADT, a destructor is generated. This is a field that extracts the given argument out of the constructor, and is only well-defined if the ADT instance is known to correspond to the given constructor.
assert Cons(1, Nil()).value == 1
assert Cons(1, Nil()).tail == Nil()
// this expression is not well-defined:
// assert Nil().value == 0
Derived methods
Similarly to derivable methods in Haskell or Rust, the ADT plugin provides a syntax to derive certain operations for ADTs.
import <adt/derives.vpr>
adt Name[...] {
...
} derives {
...
}
The block after the derives keyword is a list of functions that should be derived for the declared ADT. At the moment, the only supported operation is contains, but this may change in future Viper versions.
Note that the import <adt/derives.vpr> is required for derived methods to work.
contains
When the contains operation is derived, the function contains becomes available for the given ADT. Given a value and an ADT instance, it evaluates to true if the former value is found inside the ADT instance, as one of its constructor arguments. This evaluation works recursively.
import <adt/derives.vpr>
adt List[T] {
Nil()
Cons(value: T, tail: List[T])
} derives {
contains
}
method client() {
var x: List[Int] := Cons(42, Cons(33, Nil()))
// test for the "value" argument of type Int in x
assert contains(42, x)
assert contains(33, x)
// test for the "tail" argument of type List[Int] in x
assert contains((Nil() : List[Int]), x)
assert contains(Cons(33, Nil()), x)
}
By default, all arguments of every constructor of an ADT are considered for the contains operation. An optional comma-separated blocklist of arguments can be declared, which will cause the contains operation to ignore the named arguments:
import <adt/derives.vpr>
adt Tree[T] {
Leaf()
Node(left: Tree[T], val: T, right: Tree[T])
} derives {
contains without left, right
}
method client() {
var x: Tree[Int] := Node(Leaf(), 42, Node(Leaf(), 33, Leaf()))
assert contains(42, x)
// will fail to prove, because "right" is in the blocklist
assert contains(Node(Leaf(), 33, Leaf()), x)
}
Termination
In the context of Viper, reasoning about termination serves (at least) two purposes: the first is to prove that methods and loops terminate, the second is to ensure that Viper functions are well-defined. The second aspect is crucial even for front-ends that are not concerned with total correctness, because specifications, often expressed via Viper’s pure functions, would be meaningless if the involved functions were not well-defined.
Front-ends can encode their own termination proofs, but since proving termination is a crucial verification task with subtle pitfalls, Viper has support for termination proofs built in, based on the well-known approach of termination measures (ranking functions).
In this section, we will introduce Viper’s support for termination proofs: first, we describe how to specify termination measures, then we explain termination proofs for (mutually) recursive functions. Lastly, we discuss our experimental support for termination of methods and loops.
Termination Measures and Decreases Clauses
To prove termination of a recursive function, users must specify a termination measure: a Viper expression whose value is checked to decrease at each recursive call, with respect to a well-founded order. Termination measures are provided via decreases clauses:
decreases <tuple>
Here, <tuple> denotes the termination measure: a tuple of comma-separated expressions. In this tutorial, we interchangeably refer to <tuple> as termination measure and decreases tuple. For functions and methods, a decreases tuple can be defined at the position of a precondition, for a loop, at the position of an invariant.
A common example for termination is the standard factorial function, which terminates because its argument decreases with respect to the usual well-founded order over non-negative numbers.
import <decreases/int.vpr>
function factorial(n:Int) : Int
requires 0 <= n
decreases n
{ n == 0 ? 1 : n * factorial(n-1) }
Viper successfully verifies that factorial terminates: at each recursive invocation, it checks that 1. the termination measure n decreases and 2. remains non-negative, i.e. cannot decrease infinitely often. The corresponding well-founded order over non-negative numbers is defined in the file decreases/int.vpr, which is part of Viper’s standard library.
Hint: If you run the Viper verifier Silicon (symbolic-execution-based) with --printTranslatedProgram then you can inspect the verification conditions generated for termination checks.
Predefined Well-Founded Orders
Viper’s standard library provides definitions of well-founded orders for most types built into Viper, all of which can be imported from the decreases folder. The following table lists all provided orders; we write s1 <_ s2 if s1 is less than s2 with respect to the order.
| Build-In Type (file name) |
Provided Well-Founded Order |
|---|---|
Ref( ref.vpr) |
r1 <_ r2 <==> r1 == null && r2 != null |
Bool( bool.vpr) |
b1 <_ b2 <==> b1 == false && b2 == true |
Int( int.vpr) |
i1 <_ i2 <==> i1 < i2 && 0 <= i2 |
Rational( rational.vpr, rationals will be deprecated in the summer 2023 release): |
r1 <_ r2 <==> r1 <= r2 - 1/1 && 0/1 <= r2 |
Perm( perm.vpr) |
p1 <_ p2 <==> p1 <= p2 - write && none <= p2 |
Seq[T]( seq.vpr) |
s1 <_ s2 <==> |s1| < |s2| |
Set[T]( set.vpr) |
s1 <_ s2 <==> |s1| < |s2| |
Multiset[T]( multiset.vpr) |
s1 <_ s2 <==> |s1| < |s2| |
PredicateInstance( predicate_instance.vpr) |
p1 <_ p2 <==> nested(p1, p2) |
All definitions are straightforward, except the last one, which is concerned with using predicate instances as termination measures. Due to the least fixed-point interpretation of predicates, any predicate instance has a finite depth, i.e., can be unfolded only a finite number of times. This implies that a predicate instance p1, which is nested inside a predicate instance p2, has a smaller (and non-negative) depth than p2.
Viper uses this nesting depth to enable termination checks based on predicate instances, as illustrated by the next example, the recursive computation of the length of a linked list: intuitively, the remainder of the linked list, represented by predicate instance list(this), is used as the termination measure. This works because the recursive call is nested under the unfolding of list(this), and takes the smaller predicate instance list(this.next).
import <decreases/predicate_instance.vpr>
field next: Ref
predicate list(this: Ref) {
acc(this.next) &&
(this.next != null ==> list(this.next))
}
function length(this: Ref): Int
decreases list(this)
requires list(this)
{
unfolding list(this) in this.next == null ? 1 : 1 + length(this.next)
}
Final remarks:
- Note that
PredicateInstanceis an internal Viper type, and currently supported only in decreases tuples. Thenestedfunction is also internal and cannot be used by users. - For simplicity, all standard well-founded orders can be imported via
decreases/all.vpr. - Users can also define custom well-founded orders.
General Syntax of Decreases Tuples
In the previous examples, the termination measures were always single expressions. However, it is not always possible to find a single expression whose value decreases at each call, and Viper therefore also supports tuples of expressions as termination measures. The well-founded order for tuples is the lexicographical order over the tuple elements.
More precisely, let (a1, a2, ...) and (b1, b2, ...) be two non-empty tuples of finite (and for now, equal) length. The well-founded order <_ that is used to compare the two tuples is defined as follows:
(a1, a2, ...) <_ (b1, b2, ...)
<==>
a1 <_ b1 || a1 == b1 && (a2, ...) <_ (b2, ...)
Special cases, such as empty tuples, tuples of different length, and tuples of different types will be discussed later.
A typical example of a function for which a tuple as termination measure is used, is the Ackermann function:
import <decreases/int.vpr>
function ack(m:Int, n:Int):Int
decreases m, n
requires m >= 0
requires n >= 0
ensures result >= 0
{
m == 0 ? n + 1 :
n == 0 ? ack(m - 1, 1) :
ack(m - 1, ack(m, n - 1))
}
For the first recursive call ack(m - 1, 1), and the second (outer) recursive call ack(m - 1, ack(m, n - 1)), the first expression of the tuple (i.e. m) decreases. Hence, the other part of the tuple is not required to decrease in this situation. In the third (inner) recursive call ack(m, n - 1) the first expression of the tuple is unchanged, while the second tuple expression (i.e., n) decreases.
The well-founded order over tuples need not be imported (and cannot be customised). However, the well-founded orders of the types appearing in the tuple must be.
Special Decreases Tuples
Viper supports three decreases tuples whose semantics require further explanation.
Empty
Consider the following pair of functions, where compute performs the actual computation and facade merely provides a default argument to compute:
function facade(i: Int): Int { compute(i, 0) }
function compute(i: Int, j: Int): Int { i + j }
Both functions have no decreases clause, and Viper thus won’t generate termination checks. This may be fine now, since the functions obviously terminate, but if compute were changed to be recursive, potential non-termination might go unnoticed. To account for future code changes, users could use “artificial” constants as termination measures, but Viper offers a better solution: to ensure termination checks, users can specify empty tuples, and Viper’s call-graph analysis (performed to detect mutual recursion) effectively infers suitable constants.
function facade(i: Int): Int
decreases
{ compute(i, 0) }
function compute(i: Int, j: Int): Int
decreases
{ i + j }
- Make the body of
computerecursive, e.g., by changing it toi <= 0 ? j : compute(i - 1, j + i), and verify the program - Provide a termination measure, so that the changed program verifies again
Wildcard
Specifying a termination measure might not always be an option: it could be too cumbersome to express; it could be considered a problem to deal with later; or it could be that the function does not terminate in an operational sense, but is nevertheless well-defined. Simply omitting the decreases clause, however, might not be an option, e.g. because the function is called from another function, for which termination checks are generated.
For such cases, Viper offers the wildcard measure _, which expresses that a function is to be considered terminating, although no termination checks are generated. I.e., a wildcard measure is effectively an unchecked assumption.
function collatz(n: Int): Int
requires 1 <= n
decreases _ // I can't be bothered right now
{
n == 1 ? n :
n % 2 == 0 ? collatz(n / 2) :
collatz(3 * n + 1)
}
Star
To explicate that a function is not checked for termination, and may thus not terminate, Viper supports the star measure *. This special measure is equivalent to providing no decreases clause at all, but may be useful for documentation purposes.
function nonterm(): Int
decreases * // Whole clause could as well have been omitted
{ 1 + nonterm() }
Custom Well-Founded Orders
As previously mentioned, Viper offers predefined orders for its built-in types, plus predicates. However, via domains, Viper also enables users to define their own types. In order to use values of custom types as termination measures, users can either define a mapping from custom to some built-in type, or they can directly define a well-founded order over the custom type.
In the remainder of this subsection, both approaches will be illustrated using a combination of the MyInt example (from the earlier subsection on domains) and a factorial function operating on MyInt. In the example below, the destructor get is used to map a MyInt to a regular Int, which indirectly allows using MyInt in the function’s decreases clause.
import <decreases/int.vpr>
domain MyInt {
function put(i: Int): MyInt // Constructor
function get(m: MyInt): Int // Destructor
function dec(m: MyInt): MyInt // Decrement by one
axiom { forall i: Int :: {put(i)} get(put(i)) == i }
axiom { forall m: MyInt :: {dec(m)} dec(m) == put(get(m) - 1) }
}
function factorial(m: MyInt): Int
requires 0 <= get(m)
decreases get(m)
{ get(m) == 0 ? 1 : get(m) * factorial(dec(m)) }
Alternatively, a well-founded order for MyInt itself can be defined, by instantiating the two special functions decreasing and bounded for MyInt. The necessary function declarations are provided by the standard library file decreases/declaration.vpr, and look as follows:
domain WellFoundedOrder[T] {
// v1 is less than v2
function decreasing(v1: T, v2: T): Bool
// v is bounded
function bounded(v: T): Bool
}
Function decreasing is used to define an order between two values v1 and v2 of a custom type T, whereas function bounded is used to define a lower bound on such values. Suitable definitions for both suffices to establish a well-founded order (where, as before, <_ denotes well-founded less-than over type T):
v1 <_ v2 <==> decreasing(v1, v2) && bounded(v2)
The necessary properties of decreasing and bounded for values of type T can be defined via axioms. For the MyInt type from before, suitable axioms would be:
domain MyIntWellFoundedOrder {
axiom {
forall i1: MyInt, i2: MyInt :: {decreasing(i1, i2)}
get(i1) < get(i2) <==> decreasing(i1, i2)
}
axiom {
forall m: MyInt :: {bounded(m)}
0 <= get(m) <==> bounded(m)
}
}
- Change the
factorialfunction in the program above such that parametermis used as its termination measure. The termination check should then fail because no well-founded order forMyInthas been defined. - Add the axioms for
decreasingandbounded, to define a well-founded order forMyIntvalues. The program should verify again.
Mutual Recursion
For mutually recursive functions, Viper implements the following approach (as, e.g., Dafny does as well): given a mutually recursive function fun, Viper verifies that fun function’s termination measure decreases at each indirectly recursive call. By transitivity, this implies that the measure decreased by the time a recursive invocation of fun takes place.
A simple case of mutual recursion is illustrated next, by functions is_even and is_odd:
import <decreases/int.vpr>
function is_even(x: Int): Bool
requires x >= 0
decreases x
{
x == 0 ? true : is_odd(x-1)
}
function is_odd(y: Int): Bool
requires y >= 0
decreases y
{
y == 0 ? false : is_even(y-1)
}
Consider function is_even: its termination measure x decreases at the indirectly recursive call is_odd(x-1), where is_odd‘s termination measure y is instantiated with x-1. Analogously, is_odd‘s termination measure decreases at the call is_even(y-1).
In the example above, the two termination measures are tuples of equal length and type. However, this is not required of mutually recursive functions in order to prove their termination. Consider the next example (which verifies successfully):
import <decreases/int.vpr>
import <decreases/bool.vpr>
function fun1(y: Int, b: Bool): Int
decreases y, b
{
(b ? fun1(y, false) : 1)
+ (y > 0 ? fun2(y-1) : 2)
}
function fun2(x: Int): Int
decreases x
{
x > 0 ? fun1(x-1, true) : 3
}
At indirectly recursive calls, two decreases tuples are compared by lexicographical order of their longest commonly typed prefix (as does, e.g., Dafny). E.g., for the indirectly recursive call fun2(y-1) in function fun1, Viper verifies that y-1 <_ y, while for the recursive call fun1(y, false), it verifies that y <_ y || (y == y && false <_ b).
Comment the import of
bool.vpr, and reverify the program. Can you explain the resulting verification error?In the above example, change the call
fun1(x-1, true)tofun1(x, true)– the program still verifies. That’s because Viper appends aTopelement (an internal value of any type, larger than any other value) to each tuple, a neat trick also implemented by, e.g., Dafny and F*. Can you explain how this helps with checking termination of the callfun1(x, true)?
Conditional Termination
We previously presented three different kinds of termination measures: a tuple e1, e2, ..., wildcard (_) for “just assume that something is decreased”, and star (*) for “no termination guarantees”. It may sometimes be desirable to combine different measures, e.g., in order to reduce proof efforts by providing a concrete decreases tuple for certain invocations only, complemented with wildcard for the remaining invocations.
To account for this, Viper supports conditional termination clauses for the first two kinds of measures (tuple, wildcard):
decreases <tuple> ... if <condition>
decreases _ if <condition>
Here, <condition> is a boolean expression under which the decreases clause is considered. Omitting the condition, as in all previous examples, is equivalent to if true. Consequently, the condition false is equivalent to not providing the decreases clause at all.
The following example illustrates combined conditional termination clauses: function sign promises to decrease x if positive, and something (wildcard) if x is negative. In case x is zero, function sign does not (promise to) terminate.
import <decreases/int.vpr>
function sign(x: Int): Int
decreases x if 1 <= x
decreases _ if x <= -1
decreases * // can also simply be omitted
{
x == 0 ? sign(x) :
1 < x ? sign(x - 1) :
x < -1 ? sign(x + 1) :
x
}
function caller(x: Int): Int
decreases // must terminate
{
sign(x)
}
- Function
callerdoes not verify. Why is that? - Strengthen function
caller‘s specification to make it verify.
We refer to the condition 1 <= x of the clause decreases x if 1 <= x as the tuple condition, and to the condition x <= -1 of the clause decreases _ if x <= -1 as the wildcard condition. The disjunction of the two, i.e. 1 <= x || x <= -1, is the termination condition: the effective condition under which the function (promises to) terminate.
When verifying termination of function sign, the following happens for the recursive invocations:
sign(x): the termination check is vacuous because the invocation happens under the conditionx == 0, for whichsigndoes not promise to terminate.sign(x - 1): termination measurexis checked to decrease, since the call happens under the condition1 < x(which implies that the tuple condition held in the prestate).sign(x + 1): the termination check is again vacuous because the call happens under the conditionx < -1, which is the wildcard condition and termination is therefore assumed.
When verifying termination of function caller, the termination condition (1 <= x || x <= -1) of function sign is checked. Since it might not hold, a verification error is reported.
Abstract Functions
Termination specifications may also be provided for abstract functions, i.e., those without a body. For such functions, Viper still checks that the specifications are well-defined, which includes that pre- and postconditions terminate. Moreover, when an abstract function is invoked, the previously described call-site checks are made.
When Viper performs a call-graph analysis to determine (mutually) recursive functions, abstract functions are assumed to not (mutually) recurse through their omitted bodies.
Statement Termination (Experimental)
Termination checks outside of functions – for methods and loops, and method and function calls – are considered experimental: their semantics could change in the future, or they might be removed from Viper completely.
We encourage you to experiment with the current implementation, and to let us know if it suits your needs and whether changes or additional features would benefit your verification efforts, etc.
Function Calls inside Methods
The development of the experimental termination checks for statements was (partly) guided by Viper’s intended use as an intermediate verification language. This shaped, among other things, how function calls are currently handled.
Front-ends may use Viper functions to encode (pure) program procedures, but front-ends may also use functions to encode proof-relevant properties. Similarly, Viper methods may be used to encode (impure) program procedures, or to encode proof lemmas. Moreover, encoded program procedures could contain Viper statements corresponding to actual statements from the source program, interspersed with Viper statements that encode additional proof steps.
Consider, e.g., a Viper function elems(ll) that denotes the set of all elements in a potentially cyclic linked-list ll. A statement such as inhale es == elems(ll) could be part of a sequence of program statements – in which case elems(ll) should probably terminate – or it could be an additional proof step, in which case it would suffice if elems(ll) were well-defined.
Function calls inside Viper methods (as opposed to calls inside functions) are therefore (currently) not checked for termination, and front-ends would have to generate appropriate checks where necessary. Potential alternatives include (1) to always check termination – probably too restrictive; (2) to enable users to specify termination requirements at call-site, e.g. via attributes/annotations – but the latter are currently not available in Viper.
Checking Loop Termination
Viper while loops accept decreases clauses at the position of invariants, as illustrated by the following code snippet:
while (0 < i)
decreases i
{
i := i - 1
}
Given such a specification, Viper will check that the termination measure decreases if the loop body is executed again. A successful verification then implies that the loop is always bounded, i.e. that a finite unrolling of the loop exists. Consequently, Viper does (currently) not check that each statement, including nested loops, in the loop body terminates, as illustrated by the next code snippet:
method m() // might not terminate
while (0 < i)
decreases i // verifies successfully (finite unrolling exists)
{
i := i - 1
m()
while (true) {}
}
We have chosen this approach for the following reasons (but are happy to receive feedback and discuss alternatives):
Minimality: Interpreting loop termination as “a finite unrolling exists” can be seen as the weakest reasonable requirement, compared to the stronger (additional) requirement of all body statements having to terminate (note: the same argument does not apply to functions).
Uniformity: When proving method termination (discussed next), the current approach directly exhibits the same behaviour for both syntactic
whileloops and loops encoded viagotos andlabels (but see the note below). If loop bodies had to terminate as well, it would pose the question of which statements belonged to a goto-loop, which in general cannot be answered unambiguously (e.g. when inferring a while-loop from a goto-loop). This uniformity also extends to manually unrolled loops, as some front-ends might do.Expressiveness: If loop body termination checks are required, they can be encoded easily (potentially via a synthetic method that only hosts the loop body).
Familiarity: The same approach is used in Dafny (but then again, Dafny was not designed as an intermediate verification language)
Checking Method Termination
The currently implemented approach to checking termination of methods is similar to the previously described approach for functions: decreases clauses can be specified at the position of preconditions; if provided, Viper checks that the termination measure decreases in each directly or indirectly recursive method invocation, and that other method calls, as well as loops, terminate. As previous described, function applications inside methods are not checked for termination.
A straightforward example is method sum, shown next:
import <decreases/int.vpr>
method sum(n: Int) returns (res: Int)
requires 0 <= n
decreases
ensures res == n * (n + 1) / 2
{
res := 0
var i: Int := 0;
while (i <= n)
invariant i <= (n + 1)
invariant res == (i - 1) * i / 2
decreases n-i
{
res := res + i
i := i + 1
}
}
- Remove the decreases-clause from the loop and observe that the method no longer verifies.
- Revert to the initial program, add declaration
method m()to the program, and callminside the loop. Observe that it is (again) the method that fails to verify now. - Avoid the error by removing the decreases-clause from method
sum(or by adding a wildcard decreases-clause to methodm). - Revert to the initial program, add a nested loop, e.g.
var j: Int := n; while(0 < j) { j := j - 1 }, and observe the resulting verification failure. Experiment a bit with adding new and removing existing decreases clauses.
Final remark: Viper (currently) performs a call-graph analysis for methods to detect mutually recursive methods. Analogous to the case of functions, this is done for convenience, to unburden users from having to write “artificial” constant termination measures for non-recursive methods. This could be considered a deviation from Viper’s otherwise method-modular verification approach – please let us know if this poses a problem in your use case of Viper.
More Information
For further information about the Viper project in general, please check out the project page. This includes links to papers about the language, and about encoding a variety of verification problems into Viper. More examples to try online can be found here. However, for more serious usage of Viper, we strongly recommend downloading a version to use locally, for example via our VSCode plugin. See the project page for more details.
If you have comments, questions or feedback about Viper, including this tutorial, we would be happy to receive them! Please send your emails to viper@inf.ethz.ch
